[科普中国]-艾普塞朗数

艾普塞朗数ε乃是数学集合论中一系列的超限序数，其为指数映射的某些固定点。

简介艾普塞朗数并不能透过较小序数有限次数的加法及乘法运算而获得。康托尔原来引进的艾普塞朗数，乃以以下的方式定义:

ε乃是一个满足以下式的序数，当中ω乃是最小的无限序数。

满足上式的所有ε当中，最小的记为ε0。它可以透过以下的超限递归法获得:-

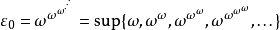其后如此类推，

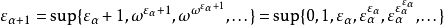更大的艾普塞朗数为

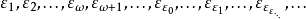
值得留意的是，ε0的基数，仍然为可数的。实际上，所有指标为可数的ε，其基数也是可数的。不可数的ε（意指满足定义式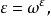 的ε）存在，但其指标也是不可数的。

超限序数超限数是大于所有有限数（但不必为绝对无限）的基数或序数，分别叫做超穷基数（英语：transfinite cardinal number）和超穷序数（英语：transfinite ordinal number）。术语“超限”（transfinite）是康托尔提出的，他希望避免词语无限（infinite）和那些只不过不是有限（finite）的那些对象有关的某些暗含。当时其他的作者少有这些疑惑；现在被接受的用法是称超限基数或序数为无限的。但是术语“超限”仍在使用。

超穷序数可以确定超穷基数，并导出阿列夫数序列。

对于有限数，有两种方式考虑超限数，作为基数和作为序数。不像有限基数和序数，超限基数和超限序数定义了不同类别的数。

1.最小超限序数是ω。

2.第一个超限基数是aleph-0 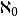，整数的无限集合的势。如果选择公理成立，下一个更高的基数是aleph-1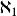。如果不成立，则有很多不可比较于aleph-1并大于aleph-0的其他基数。但是在任何情况下，没有基数大于aleph-0并小于aleph-1。

连续统假设声称在aleph-0和连续统（实数的集合）的势之间没有中间基数：就是说，aleph-1是实数集合的势。已经在数学上证实了连续统假设不能被证明为真或假，由于不完备性的影响。1

某些作者，比如Suppes、Rubin使用术语超限基数来称呼戴德金无限集合的势，在可以不等于无限基数的上下文中；就是说在不假定可数选择公理成立的上下文中。给定这个定义，下列是等价的：

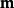是超限基数。就是说有一个戴德金无限集合A使得A的势是。

。

。

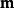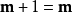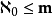有一个基数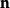使得。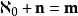

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学