[科普中国]-分片段

在数学中，分片段定义的函数（也称为分段函数或混合函数）是一个函数，是通过多个子函数而定义的，施加到主函数的域的一定的时间间隔的每个子函数（子域）。分片段实际上是一种表达函数的方式，而不是函数本身的一个特征，但是具有额外的限定，可以描述函数的本质。例如，分段多项式函数是在其每个子域上是多项式的函数，但是每个子域上可能是不同的。 字分段也用来描述适用于每件分段定义的函数的任何属性，但不一定保持为函数的整个域。一个函数是分段微分的或分段连续微分的，如果每个子块在整个子域内是可区分的，即使整个函数在块之间的点上可能是不可区分的。在凸分析中，导数的概念可以被分段函数的子导数的概念取代。尽管分段定义中的“块”不一定是间隔，但是除非是间隔，否则函数不被称为“分段线性”或“分段连续”或“分段可微”。

符号和解释分片段函数使用通用函数表示法来定义，其中函数的主体是函数和相关子域的数组。至关重要的是，在大多数情况下，只有有限数量的子域，每个子域必须是一个区间，以便将整个函数称为“分片段”。例如，考虑绝对值函数的分片段定义：

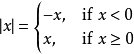对于x小于零的所有值，使用第一个函数（ - x），它将取消输入值的符号，使负数为正数。对于x大于或等于零的所有值，使用第二个函数（x），它对输入值本身进行简单计算。 考虑分片段函数f（x）在x的特定值处计算：

|| ||

连续性在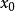两侧由不同二次函数组成的分片段函数1

如果满足以下条件，则分片段函数在给定的时间间隔内是连续的：

它在整个间隔中被定义

其构成函数在该间隔上是连续的

在该区间内的子域的每个端点处不存在不连续性。

例如，图中的函数在其子域中是分段连续的，但在整个域中是不连续的。图中的函数包含跳跃不连续性。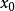

应用在应用的数学分析中，已经发现分片段函数与人类视觉系统的许多模型一致，其中在第一阶段将图像感知为包括由边缘分隔的平滑区域。特别是，剪切片已经被用作表示系统来提供2D和3D中该模型类的稀疏近似。

常见示例分片段函数的具体实例包括：

阶跃函数, 由常量函数组成的分片段函数

Boxcar function,

单位阶跃函数

符号函数

Piecewise linear function, 由线段组成的分片段函数

绝对值

破碎的幂定律, 由幂定律组成的分片段函数

样条函数, 由多项式函数组成的分片段函数，在多项式片段连接处具有高度的平滑度

B-样条

PDIFF

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学