[科普中国]-W三角数

W三角数是一种重要的形数，由n个三角形数表称为n元集的k组划分数排列成的一个三角形数表称为W三角数表。三角形数表由霍克(Hok, W.)首先发现，故以霍克的名字的第一个字母W命名。

简介W三角数是一种重要的形数，由n个三角形数表称为n元集的k组划分数排列成的一个三角形数表称为W三角数表。

三角形数表由霍克(Hok, W.)首先发现，故以霍克的名字的第一个字母W命名。

数表W三角数表如下：

此数表可不断延续下去，数表的第n行是n个元素的集合的k组划分数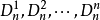。例如，第5行第3个数字25为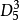，表示把5个不同元素分成三组有25种划分法。

数表特点W三角数表有下列特点：

1、三角数表“两腰”上的数全为1；

2、不在两腰上的每个数x可由它的“两肩”上的两数按下述法则计算得到：x=x左肩上的数+x在行中的序数×x右肩上的数。例如，第6行第3个数90为15+3×25。

3.第n行中数字的和是n个元素的划分数Dn。例如，由第4行可得D4=1+7+6+1=15。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学