[科普中国]-k阶中值定理

k阶中值定理是微分中值定理的推广。

简介k阶中值定理是微分中值定理的推广。

若f:[a,b]→R在[a,b]上k次可微，h=(b-a)/k，则存在ξ∈(a,b)，使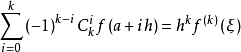。1

应用如果函数f二阶连续可微，即∇2f(x)存在且连续，那么就有二阶Taylor展开和二阶中值定理。

特别地，对任意x和y有f(x+y)=f(x)+y'∇f(x)+0.5y'∇2f(x)y+o(|lyll2)，同时存在α∈[0,1]，使得f(x+y)=f(x)+y'∇f(x)+0.5∇2f(x+αy)y。2

微分中值定理微分中值定理是一系列中值定理总称，是研究函数的有力工具，其中最重要的内容是拉格朗日定理，可以说其他中值定理都是拉格朗日中值定理的特殊情况或推广。微分中值定理反映了导数的局部性与函数的整体性之间的关系，应用十分广泛。

微分中值定理包括罗尔定理、拉格朗日定理、柯西定理、泰勒公式、达布定理、洛必达法则等。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学