[科普中国]-欧拉级数

欧拉级数是各项为质数倒数的级数，欧拉（Euler，L.）于1748年证明了欧拉级数是发散的，同时给了质数集是无穷集的一个证明。

简介欧拉级数是各项为质数倒数的级数，即级数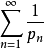，式中pn为第n个质数。

背景欧拉（Euler，L.）于1748年证明了欧拉级数是发散的，同时给了质数集是无穷集的一个证明。

对欧拉级数的部分和成立着渐近等式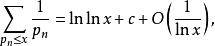其中，c=0.261497...1

级数级数是指将数列的项依次用加号连接起来的函数。典型的级数有正项级数、交错级数、幂级数、傅里叶级数等。

级数理论是分析学的一个分支；它与另一个分支微积分学一起作为基础知识和工具出现在其余各分支中。二者共同以极限为基本工具，分别从离散与连续两个方面，结合起来研究分析学的对象，即变量之间的依赖关系──函数。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学