高能粒子相互作用的过程,通常称之谓散射。引入一个算散算符S,就可用来描述粒子初态和末态之间的转变。从而通过对于散射算符矩阵元的计算,就可得到相应的几率幅。
散射算符在量子物理中,描述微观粒子的运动方程为薛定谔方程

式中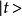 为时刻t系统的态矢,H为系统的总的哈密顿量。若系统是封闭的,则哈密顿量H与时间无关。此外,在量子场论中,算符对应于一个物理量,其期待值为:
为时刻t系统的态矢,H为系统的总的哈密顿量。若系统是封闭的,则哈密顿量H与时间无关。此外,在量子场论中,算符对应于一个物理量,其期待值为:
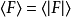 式中F为对应于某一物理量的算符。当系统有相互作用时,总的哈密顿量H,假定可以分解为“无微扰”的
式中F为对应于某一物理量的算符。当系统有相互作用时,总的哈密顿量H,假定可以分解为“无微扰”的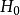 和“有微扰”的
和“有微扰”的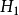 两部分,即有:
两部分,即有:
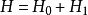 为了满足明显的协变性的要求和便于求解起见,在量子场论中,通常采用相互作用绘景。为此,我们只需对态矢和物理量进行一个么正变换,就可导出汤川秀树一史温格方程:
为了满足明显的协变性的要求和便于求解起见,在量子场论中,通常采用相互作用绘景。为此,我们只需对态矢和物理量进行一个么正变换,就可导出汤川秀树一史温格方程:
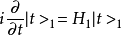 式中
式中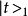 为相互作用绘景中之态矢。而
为相互作用绘景中之态矢。而
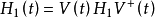
为变换后的相互作用哈密顿量。为么正算符,变换后的任何物理量算符均可写为:
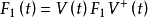
并满足力学量的对易关系。而几率却与变换无关
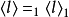
算符期待值,也不因绘景的改变而改变,
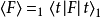
在不同绘景中的态矢,在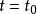 时,应该是一致的。所以,通常可以选取
时,应该是一致的。所以,通常可以选取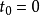 ,或
,或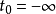 。因为在相互作用绘景图中,有
。因为在相互作用绘景图中,有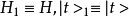 。
。
对于散射过程,先定义一个算符S,使之有
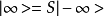 式中算符S,称为散射算符1。
式中算符S,称为散射算符1。
性质;1.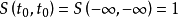
2.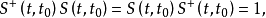 即
即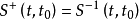
3.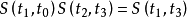
4.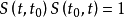 ,即
,即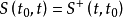
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国