[科普中国]-施托尔茨极限定理

施托尔茨极限定理是给出求极限的一种方法的命题。施托尔茨极限定理对函数极限也可得出类似结论。

简介施托尔茨极限定理是给出求极限的一种方法的命题。1该定理断言：

若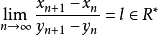，且满足下列条件中的一个：

1、{yn}严格增，yn→+∞（或{yn}严格减）

2、xn→0，yn→0，{yn}严格减

则

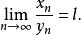
对函数极限的结论施托尔茨极限定理对函数极限的类似结论如下：

设f:(a,+∞)→R在任意有限区间(a,b)内有界；当x→+∞时，g(x)→+∞，且g(x)严格单调增，若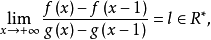则

函数极限函数极限是高等数学最基本的概念之一，导数等概念都是在函数极限的定义上完成的。

函数极限性质的合理运用。常用的函数极限的性质有函数极限的唯一性、局部有界性、保序性以及函数极限的运算法则和复合函数的极限等等。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学