[科普中国]-方向极限

点（自变量）沿一射线变动时函数的极限称为方向极限，即在Rn中，自变量x沿某方向趋于a时函数的极限。

简介点（自变量）沿一射线变动时函数的极限称为方向极限，即在Rn中，自变量x沿某方向趋于a时函数的极限。

性质在Rn中，当：

n=1时，只有两种方式：x沿x轴从左方或从右方趋于a，这时得到左、右极限。

当n>1时，有无穷个方向极限：若x沿方向向量为v的直线趋于a，则直线方程为x=a+tv，方向极限可表示为。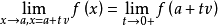

当n=2且a=0时，v=(cosθ,sinθ)，(x,y)→(0,0)的方向极限可表示为

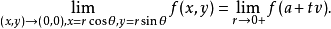
n>1时，从重极限存在可知（在同一点）所有方向极限存在且相等，反之不然。1

方向向量空间直线的方向用一个与该直线平行的非零向量来表示，该向量称为这条直线的一个方向向量。直线在空间中的位置， 由它经过的空间一点及它的一个方向向量完全确定。

已知定点P0（x0,y0,z0)及非零向量v={l,m,n}，则经过点Pο且与v平行的直线L就被确定下来，因此，点P0与v是确定直线L的两个要素，v称为L的方向向量。

由于对向量的模长没有要求，所以每条直线的方向向量都有无数个。直线上任一向量都平行于该直线的方向向量。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学