[科普中国]-欧拉代换

欧拉代换是求积分时常用的一种代换，有三种情形，三种欧拉代换都是有理代换，在相应情况下分别使用它们，都能使被积函数有理化1。

基本介绍形如

的不定积分(a≠0且没有重根，否则归于有理函数的积分)，可经配方后再用三角代换化为三角有理式计算。欧拉代换是一种直接把被积表达式有理化的方法。分下列三种情形。

说明：下面所考虑的三种情况，已包含了所有的可能。因若欧拉第三代换不满足，即二次三项式无实根，则必b2-4ac0，又必同时c>0，否则b2-4ac≥o．这就是说，不属于欧拉第三代换，必属于欧拉第一代换2。

欧拉第一代换设a>0，令

或

可将被积表达式有理化2。

欧拉第二代换设c>0，令

或

可将被积表达式有理化2。

欧拉第三代换设其中是二次三项式的两个实根，，令

或

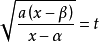可将被积表达式有理化2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学