[科普中国]-对称导数

对称导数是导数的一种推广。对称导数常特指二阶对称导数，它是黎曼（Riceman，(G.F.)B.）于1854年研究三角级数时首先引进的，后来由施瓦兹（Schwarz，H.A.）详细研究过，故又称为黎曼导数或施瓦兹对称导数。

简介对称导数是导数的一种推广。

对称导数常特指二阶对称导数，它是黎曼（Riceman，(G.F.)B.）于1854年研究三角级数时首先引进的，后来由施瓦兹（Schwarz，H.A.）详细研究过，故又称为黎曼导数或施瓦兹对称导数。

举例设一元函数f在x附近有定义，f在x处的：

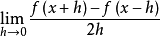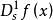一阶对称导数是数，记为或；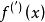

二阶对称导数是数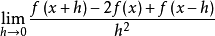，记为或。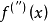

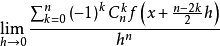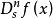n阶对称导数为，记为或。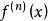

对称差n阶对称导数分式中的分子记为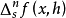，称为f在x处的n阶对称差。记号中的s是symmetric（对称）的第一个字母。

f可微时，f(')存在且等于f'，反之不然，如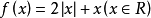，当f与f(')均连续时f可微。1

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学