[科普中国]-广义傅里叶级数

广义傅里叶级数(generalized Fourier series)是特殊的正交级数，函数f(r)在区间[0，a]上具有二阶连续导数，则f(r)可以展开成以贝塞尔函数为基的广义傅里叶级数1。

基本介绍对于定义在区间[-1，1]上的具有二阶连续导数的函数f(x)，当它与P，(z)具有相同的边界条件时，可按Pl(x)展为绝对且一致收敛的级数，

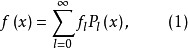称之为广义傅里叶级数。{Pl(x)}可以看作广义傅里叶级数展开的基，这说明勒让德多项式(Pl(x))是完备的2。

在式(1)两端乘以Pk(x)并在区间[-1，1]上积分，利用正交归一性，得

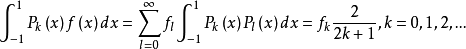于是，得广义傅里叶系数

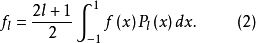
如果将变量x换回θ，则式(1)和式(2)变为

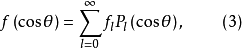
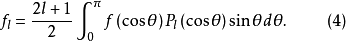
例题解析【例1】以勒让德多项式为基，在[-1，1]上将函数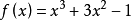 展为广义傅里叶级数。

解：这里我们当然可以按照式(1)和式(2)将f(x)展开，但是由于f(x)是比较简单的三次多项式形式，应该可以表示为P0(x)，P1(x)，P2(x)和P3(x)的线性组合，从而可以利用待定系数法确定广义傅里叶系数，不妨设2

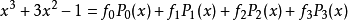
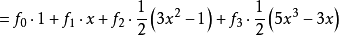
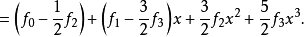比较两端系数，得

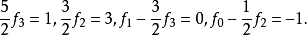于是，

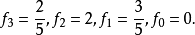因此，

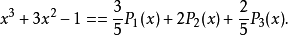
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学