[科普中国]-零导数定理

零导数定理是可微函数为常值函数的充分必要条件。若一元函数f在区间I上连续，在I的内部可微，则f为I上为常值函数的充分必要条件是f'=0。

简介零导数定理是可微函数为常值函数的充分必要条件。

若一元函数f在区间I上连续，在I的内部可微，则f为I上为常值函数的充分必要条件是f'=0。

条件零导数定理的条件可以减弱为：在I上连续，除可数个点外存在等于零的右导数。

一般地，对向量值函数。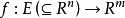

若E是连通开集，则f为常值的充要条件是：对任意x∈E，有Df(x)=0，即对任意i=1,2,...,m，j=1,2,...,n，Djfi(x)=0。特别地，当m=1时，条件成为grad f=0。

定义域零导数定理中，f的定义域的连通性是必不可少的。

例如：设m=n=1，E=(-2,-1)U(0,1)，且x∈(-2,-1)时，f(x)=1，x∈(0,1)时，f(x)=0，则f'=0，但f非常值。

Rn和Rm换成任意赋范线性空间时这个定理仍成立。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学