算术-几何平均值不等式,简称算几不等式,是一个常见而基本的不等式,表现了算术平均数和几何平均数之间恒定的不等关系。
介绍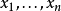 算术-几何平均值不等式,简称算几不等式,是一个常见而基本的不等式,表现了算术平均数和几何平均数之间恒定的不等关系。设
算术-几何平均值不等式,简称算几不等式,是一个常见而基本的不等式,表现了算术平均数和几何平均数之间恒定的不等关系。设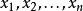 为n个正实数,它们的算术平均数是
为n个正实数,它们的算术平均数是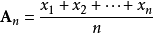 ,它们的几何平均数是
,它们的几何平均数是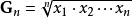 。算术-几何平均值不等式表明,对任意的正实数,总有:
。算术-几何平均值不等式表明,对任意的正实数,总有:
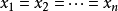
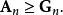 等号成立当且仅当。
等号成立当且仅当。
算术-几何平均值不等式仅适用于正实数,是对数函数之凹性的体现,在数学、自然科学、工程科学以及经济学等其它学科都有应用。
算术-几何平均值不等式有时被称为平均值不等式(或均值不等式),其实后者是一组更广泛的不等式。
证明使用常规数学归纳法的证明则有乔治·克里斯托(George Chrystal)在其著作《代数论》(algebra)的第二卷中给出的:1
由对称性不妨设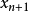 是
是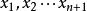 中最大的,由于
中最大的,由于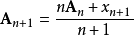 ,设
,设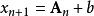 ,则
,则 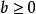 ,并且有
,并且有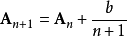 。
。
根据二项式定理,

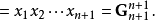
于是完成了从n到n+1的证明。
例子在n=4 的情况,设: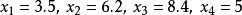 , 那么2
, 那么2
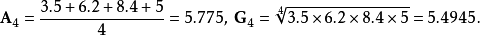 可见
可见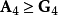 。
。
推广不仅“均匀”的算术平均数和几何平均数之间有不等式,加权的算术平均数和几何平均数之间也有不等式。设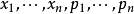 为正实数,并且
为正实数,并且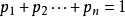 ,那么:
,那么:
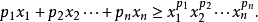 加权算术-几何平均不等式可以由琴生不等式得到。
加权算术-几何平均不等式可以由琴生不等式得到。
参见平均数不等式
算术平均数
几何平均数
幂平均不等式
杨氏不等式
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国