汉克尔变换是指对任何给定函数 以第一类贝塞尔函数作无穷级数展开,贝塞尔函数 的阶数不变,级数各项作变化1。
定义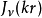 汉克尔变换是指对任何给定函数
汉克尔变换是指对任何给定函数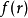 以第一类贝塞尔函数作无穷级数展开,贝塞尔函数
以第一类贝塞尔函数作无穷级数展开,贝塞尔函数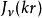 的阶数不变,级数各项
的阶数不变,级数各项 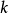 作变化。各项
作变化。各项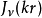 前系数
前系数 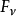 构成了变换函数。对于函数
构成了变换函数。对于函数 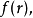 其
其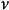 阶贝塞尔函数的汉克尔变换(
阶贝塞尔函数的汉克尔变换(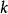 为自变量)为
为自变量)为
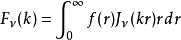 其中,
其中,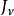 为阶数为
为阶数为 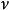 的第一类贝塞尔函数,
的第一类贝塞尔函数,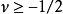 。对应的,逆汉克尔变换
。对应的,逆汉克尔变换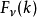 定义为
定义为
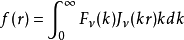 汉克尔变换是一种积分变换,最早由德国数学家 Hermann Hankel 提出,又被称为傅立叶-贝塞尔变换。
汉克尔变换是一种积分变换,最早由德国数学家 Hermann Hankel 提出,又被称为傅立叶-贝塞尔变换。
正交性贝塞尔函数构成正交函数族权重因子为r:
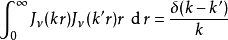 其中
其中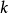 与
与 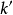 大于零。
大于零。
与其他函数变换的关系傅立叶变换零阶汉克尔函数即为圆对称函数的二维傅立叶变换2。给定二维函数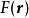 ,径向矢量为
,径向矢量为 ,其傅立叶变换为
,其傅立叶变换为
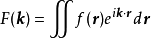 不失一般性,选择极坐标
不失一般性,选择极坐标 ,使得矢量
,使得矢量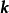 方向指向
方向指向 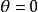 。极坐标下的傅立叶变换写作
。极坐标下的傅立叶变换写作
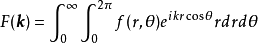 其中
其中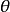 为矢量
为矢量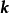 与
与 间夹角。如果函数
间夹角。如果函数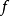 恰为圆对称不依赖角变量
恰为圆对称不依赖角变量 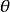 ,
,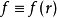 ,对角度
,对角度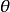 的积分可以提出,傅立叶变换写作
的积分可以提出,傅立叶变换写作
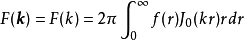 此式恰为
此式恰为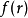 的零阶汉克尔变换的
的零阶汉克尔变换的 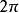 倍。
倍。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国