[科普中国]-第二型曲线积分

第二型曲线积分亦称关于坐标的曲线积分，是一种与曲线定向有关的曲线积分，与第一型曲线积分相比，从物理意义上，可以看出两种曲线积分是不同的，尽管它们都是沿着曲线的积分，但第一型的与方向无关，第二型的与方向有关。第二型曲线积分在向量场理论中还有许多应用。

第二型曲线积分的物理意义第二型曲线积分的物理背景是变力沿曲线做功。

空间中有一变力F(x，y，z)=(P(x，y，z)，Q(x，y，z)，R(x，y，z))作用在某质点上，使其从某一曲线L的端点A，沿着L移动到另一端点B，求该力做功多少？

显然在L上取一有向弧微元ds=(dx，dy，dz)，则可得做功微元dw=F·ds，那么力F移动质点从A到B所做的功为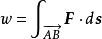 ，若用坐标表示，则成为

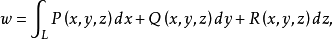这种类型的积分称为第二型的曲线积分1。

第二型曲线积分的定义定义1设函数P(x，y)，Q(x，y)定义在平面有向可求长度曲线L上，对L的任意分割T，它把L分成n个小弧段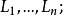： 在每个小曲线段上任取一点 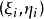，若极限

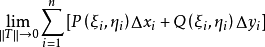存在，且与分割T和点 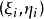的取法无关，其中||T||是各小弧段长度的最大值，则称此极限为函数P(x，y)，Q(x，y)沿有向曲线L上的第二型曲线积分，记为

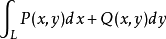或

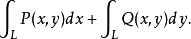
定义2 设L为空间内一条光滑有向曲线，函数P(x，y，z)，Q(x，y，z)，R(x，y，z)在L上有定义，则可以定义沿空间有向曲线L上的第二型曲线积分，并记为2

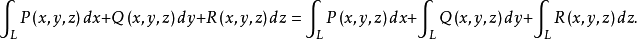
第二型曲线积分的性质(1)如果把L分成L₁和L₂，且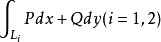 (i=l，2)都存在，则

(2)设L是有向曲线弧，-L是与L方向相反的有向曲线弧，则

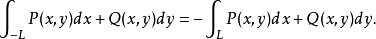
(3)若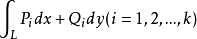 存在，则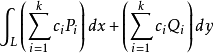 也存在，且2

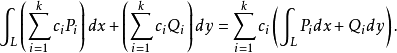
第二型曲线积分的计算转化为定积分，要注意的是：二型线积分的起点，对应定积分的下限，终点对应定积分的上限，即若曲线1

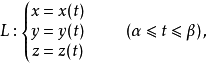则

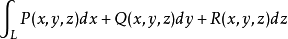
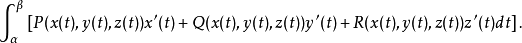
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学