[科普中国]-重叠-存储之卷积法

重叠-存储之卷积法 ( Overlap-save method, Overlap-discard method ) 是一种区块卷积 ( block convolution, sectioned convolution )，可以有效的计算一个很长的信号 x[n] 和一个 FIR 滤波器 h[n] 的离散卷积。1

定义定义信号 x[n] 和一个 FIR 滤波器 h[n] 的离散卷积：

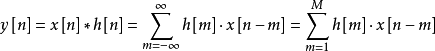
其中h[m] 在 [1,M] 之外为零。与重叠-相加之卷积法2不同之处在于，重叠-存储之卷积法所算出的输出区块并不重叠 (因此计算上少了将输出区块相加所需的加法)，而是每次用的输入区块有所重叠。因此实现时每次读取输入后需将和下一个输入重叠的部分存储起来，作为下一输入区块的开头部分，因此称为重叠-存储之卷积法。另外重叠-存储之卷积法也不需补零。

算法概念上，这个做法是选用一个较短的适当长度 L 来切割 y[n] ，则因为 h[n] 是有限长度，因此在某一区块内的 y[n] 也只被有限长的 x[n] 区块（会比 y[n] 分区成的区块长一点）所决定。因此只要选择有影响的输入区块和 h[n] 卷积，再选择结果中适当的部分即可得到正确的输出区块。

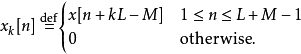
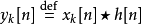
则对于在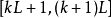 内的n， 输出y[n] 可写成

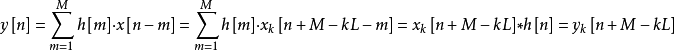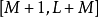所以只需计算n在 中的yk[n+M-kL] ，亦即n在 的yk[n] 部分即可。因此每一段输出区块yk[n] 的前M-1 点可丢弃（discard）。

尽管一时看不出切割成区块的好处为何，但将xk[n] 做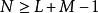 的周期延伸，

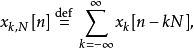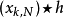则 和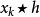 这两个卷积在 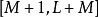的部分相等。所以可以将线性卷积改以 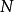点循环卷积计算，结果的 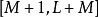部分作为输出 y[n] 在 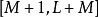的部分。由于每段xk[n] 原本就有 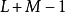长，所以选择 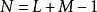的话输入 x[n] 就不需补零。 改以循环卷积计算后即可藉循环卷积定理。

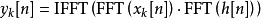
变换成三次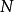 点快速傅里叶变换和 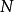次乘法，使原本每段 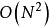的运算量减少至 O(N logN)，速度大幅增加。

准代码 (Overlap-save algorithm for linear convolution) //////// revised by fantastic //////// N = length(x), M = length(h) O = M – 1; // overlap length must be M-1 L = M; // >=1 is OK P = O + L; H = FFT(h, P); // just calc once idx = - (O - 1); // starting index which is offset M-1 in matlab while (idx = 1 i2 = min(N, idx+P-1); // must be