[科普中国]-无差别关系

无差别关系(indifference relation)是一种二元关系，指集合A上的弱优选关系Q与它的逆关系Q-1的交，A上的无差别关系记为I，对任何a，b∈A，aIb成立，当且仅当aQb且bQa，aIb的直观意义是“a在b之先，且b在a之先”，故I有无差别关系之名1。

无差别关系的性质无差别关系具有下列性质(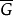 是强优选关系G的补关系)：

1.自反性：对任何a∈A，aIa。

2.对称性：对任何a，b∈A，若aIb，则bIa。

3.传递性：对任何a，b，c∈A，若aIb，bIc，则aIc。

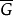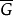4.对任何a，b∈A，若aIb，则a b且b a。

5.对任何a，b，c∈A，若aIb，且bGc， 则aGc。

6.对任何a，b，c∈A，若aIb，且cGa，则cGb。

7.对任何a，b，c，d∈A，若aGb且bIc且cGd，则aGd1。

相关介绍为了描述优先关系，通常在数学上要用序(Order)的概念。序的概念涉及到二元关系2。

设有一组元素x.y,z,...,w组成的集合X,在非空集X中的二元关系R，是X中所有有序对的乘积集X×X={(x, y)|x,y∈X}的一个子集。我们用xRy表示(x，y)有关系R(或记作(x,y)∈R),类似地用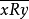 表示(x,y)没有关系(或记作(x，y)∈R)。二元关系有下述八种可能的性质，可分成四组。

自反性(reflexivity)：xRx；

非自反性(irreflexivity)： ；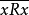

对称性(Symmetry)：若xRy,则yRx；

非对称性(asymmetry)：若xRy,则 ；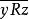

可递性(transitivity)：若xRy和yRz,则xRz；

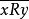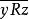负可递性(negative transitivity)：若 和 , 则 ；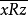

连接性(connectedness)：xRy或yRx；

弱连接性(weak connectedness)：若x≠y,则有xRy或yRx2。

任意给定一个关系， 当然不可能同时具有上述性质，而只是其中一部分性质。其中某些性质如第一对性质不可能同时兼有，而后三对却可以。例如具有非对称和负可递性就意味着有可递性。有连接性就一定有弱连接性。当R是空集时，对称性和非对称性同时成立；但当R非空时，这两个性质就不能兼有等等。例如，设X是所有居民的集合，“某高于某”的关系就具有非自反性、非对称性、 可递性和负可递性。“某和某一样年纪”的关系具有自反性、可递性。“某和某是姐妹(至少父母中有一个是共同的)”的关系是对称的， 但不一定是可递的(除非要求父母都相同!)。

可递的二元关系称为序关系或有序。满足上述某些性质的关系可以叫作各种序集。上述“年龄相同”是一种特殊的二元关系， 称为无差别关系。如果把“优先”作为原始的二元关系，就可以推出“无差别”及“优先或无差别”关系。符号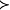 表示优先，~表示无差别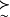， 表示优先或无差别。

若x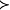 y (读为x优先于y)为原始的二元关系，则

x~ y，当且仅当非(x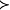 y) 以及非(y 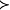x)；

x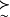 y，当且仅当x 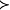y，或非(x 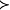y)及非(y 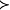x)。

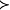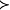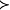如果以 作为原始的二元关系，则它是非自反的，非对称的，否则就会可能出现同时有y x及x y，还有x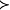 x，这都是不可能的2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学