[科普中国]-阿佩尔序列

在数学中，阿佩尔序列是得名于十九世纪法国数学家保罗·埃米尔·阿佩尔（Paul Émile Appell）的一类多项式序列。

定义阿佩尔序列满足以下关系：

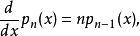其中的p0(x) 是非零常数。

除了一些平凡的例子如 {x} 以外，最值得注意的阿佩尔序列是埃尔米特多项式、伯努利多项式以及欧拉多项式。所有的阿佩尔序列都是谢弗序列，但要注意的是绝大多数谢弗序列都不是阿佩尔序列。

等价的阿佩尔序列定义方式最常见的阿佩尔序列的定义就是以上的1

对所有的n= 1, 2, 3, ...,

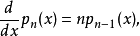
并且p0(x) 是一个非零常数

的关系式。此外，以下的条件也可以被验证是与之等价的：

纯数数列 {cn}n=0,1,2,...满足c0≠0，并且

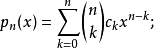
纯数数列 {cn}n=0,1,2,...满足c0≠0，并且

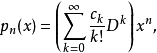其中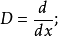

对所有的n= 0, 1, 2, ...,

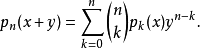
递归公式假设

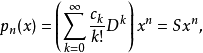
其中后一个等式是在以x为不定元的多项式构成的线性空间中的线性算子S的定义式。并定义2：

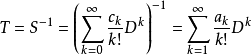
为S的逆算子，其中的系数ak是形式幂级数的逆系数。这样得到

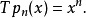在影子演算的约定中，算子T一般被用来代表阿佩尔序列 {pn}，可以定义对数算子：

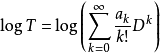运用通常的 log(1+x) 的幂级数展开表达式以及通常的复合形式幂级数定义后，可以得到：

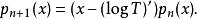当阿佩尔序列是埃尔米特多项式的时候，这个关系式也可以变化为埃尔米特多项式的递推公式。

参见谢弗序列

影子演算

广义阿佩尔多项式

Wick积

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学