[科普中国]-达布连续函数

达布连续函数(Darboux continuous function)是一种具有介值性的函数，即具有下列性质的函数：介于任意两个函数值之间的任意数都是该函数的函数值，这个性质又称函数的介值性。即：对于区间I及函数f∶I→R，若对任意x₁，x₂∈I及f(x₁)与f(x₂)之间的任何k，存在x₁与x₂之间的x0，使f(x0)=k，则称f在I上达布连续1。

基本介绍定义 所谓函数f在[a，b]上具有介值性，是指任意x₁，x₂∈[a，b]，y是介于f(x₁)与f(x₂)之间的任意一个数，则总有x₃介于x₁与x₂之间，使y=f(x₃)．这时我们称f在[a，b]上是Darboux函数，简称D函数，记为f∈D。

所谓函数f具有无穷介值性，记为f∈D*是指上述定义中，有无穷多个x₃，介于x₁与x₂之间，使y=f(x₃)。

所谓函数f具有c介值性，记为f∈D**是指上述定义中，有c个x₃，介于x₁与x₂之间，使y=f(x₃)，其中c为连续统之势。

因为连续函数具有介值性，故有关系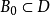，具有c介值性必有无穷介值性更有介值性，因此。

【例1】 连续函数有介值性，但有介值性函数未必连续。如函数

具有介值性，但在0点不连续，(o，1]中没有无穷介值性，更无c介值性。

设P为[0，1]中Cantor集，{(an，bn)}为P的接邻区间全体，f与g为：

则f∈D，但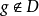。而f，g在P上都是不连续的2。

达布连续函数的性质1.由介值定理，定义在区间上的连续函数必是达布连续的，但反之不一定成立。

例如，由f(x)=sin(1/x)(x≠0)与f(0)=0定义在[-1，1]上的函数f达布连续，但在x=0处不连续。

2.f：[a，b]→R达布连续的充分必要条件是f把[a，b]的任何闭子区间映为区间或一个点。

3.达布连续函数的复合是达布连续的，因此，f(x)达布连续时，|f(x)|，f(x)，cf(x) (c∈R)，1/f(x) (f(x)≠0)也达布连续。

4.对于单调函数而言，达布连续与连续是等价的。

5.若f：R→R，且f在每个x∈R处的左、右极限存在，则f达布连续当且仅当f连续。

6.达布连续函数之和不一定达布连续。

7.达布连续函数列的一致极限不一定达布连续。

8.达布连续函数没有第一类间断点。

9.一个函数的导函数必达布连续(达布定理)。

10.任何函数f∶R→R是两个达布连续函数之差。

历史上有些数学家曾以为介值性与连续性是等价的，达布((J.-)G.Darboux)澄清了这两个概念的差别1。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学