[科普中国]-二重级数

给定带有两个下标i和j的无穷数集{aij}(i=1,2,...;j=1,2,...)，称记号a11+a12+...+a21+a22+...+a31+a32+...是二重级数(double series)。二重级数可以很方便地写成有无穷多行无穷多列的表的形式。若aij是数，则级数叫做数值二重级数；若aij是函数，则级数叫做函数项二重级数1。

基本介绍二重级数是二重序列的形式和，设{amn}是二重序列，把它的项按任意次序排列并以加号连结得到的表达式称为二重级数，记为：

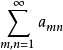， (1)

这里m，n各自独立地取正整数1，2，3，…数：

Smn=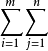aij

称为(1)的部分和2。

二重级数的相关性质二重级数的收敛性若二重极限：

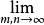Smn=S(有限)，

则称该二重级数收敛，S为它的和，记为：

S=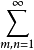amn.

当这样的S不存在时，称这个二重级数发散，若：

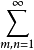|amn|

收敛，则称(1)绝对收敛，类似于通常的级数(相对于二重级数，通常的级数称为单级数)，可定义二重级数的条件收敛性，单级数的一些基本性质仍为二重级数所保持，例如，非负项二重级数收敛当且仅当其部分和有界，二重级数收敛的必要条件是amn→0(m，n→∞)，绝对收敛的二重级数必收敛(参见“绝对收敛级数”)等，对二重函数项级数，也可如函数项级数那样引进一致收敛概念，并得到相应的柯西准则、M判别法等2。

重排定理设φ是正整数集N+到N+×N+上的一一对应，则对二重级数(1)，可以得到级数：

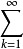aφ(k).

φ称为二重序列{amn}到序列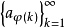的重排，或二重级数(1)到单级数∑aφ(k)的重排。若级数

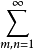|amn|，|amn|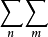，|amn|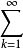，|aφ(k)|

之一收敛，则：

1.另三个也收敛，且它们的和相等(设为S)；

2.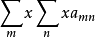与均绝对收敛于S(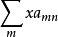与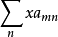也绝对收敛)。

在一些文献中，上述结论被称为主要重排定理。由此可知，绝对收敛的二重级数的两个叠级数也绝对收敛，有同一个和。由于二重级数的项的排列次序不惟一以及多种研究目的，因此，还有多种定义二重级数的部分和的方式，相应地也就有了不同的定义二重级数的和与收敛性的方式2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学