[科普中国]-希尔伯特不等式

希尔伯特不等式(Hilbert inequality)是有关双指标和或重级数的一种不等式及其推广，它是希尔伯特(D.Hilbert)于1888年提出的，关于有限和的不等式。

基本介绍希尔伯特不等式是有关双指标和或重级数的一种不等式及其推广，关于有限和的下列不等式

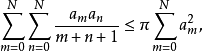其中a1，a2，…，aN≥0，它是希尔伯特(D.Hilbert)于1888年提出的，等号当且仅当a1=a2=…=aN=0时成立，π可以用更小的数

代替。更精确些，有

其中cN=π-π5/2(lnN)-2+O(lnlnN(lnN)-3)(N→∞)是最好的。令N→∞，得：

apn1/p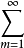 bqm1/q，

(p>1，1/p+1/q=1，an≥0，bn≥0，n=1，2，…)，常数π/sin(π/p)是最好的。它的积分类似是

其中f，g非负，p，q同上。希尔伯特不等式有许多推广，同时还可找到许多希尔伯特型不等式。如

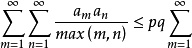apn1/p 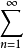bqn1/q，

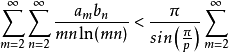apm1/p 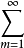bqn1/q，

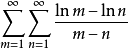ambm≤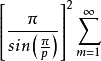 apm1/pbqn1/q，

它们也有明显的积分类似1。

相关定理定理1 若p>1，1/p+1/q=1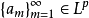，和是非负序列，且

则

除非所有am皆为零或所有bn皆为零2。

下面是关于一类较为广泛的双线性型的一个结论，它能导出定理1。

定理2 若p>1，1/p+1/q=1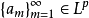，和是非负序列，K是二元函数，具有如下性质2：

(1)K为非负，且为一1次齐次式；

(2)；

(3)在(2)中的两个被积函数均为严格递减。或者，条件更弱些，(2)中的两个被积函数在区间(1，∞)上为严格递减，而区间(0，1)可分成两部分：(0，ξ)和(ξ，1)，其中有一个可以为空集，在(0，ξ)上函数为严格递减，在(ξ，1)上函数为严格递增；

(4)当K(x，x)无意义时，规定K(x，x)=0。

则

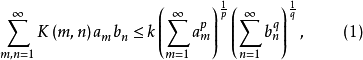等号成立仅当所有am皆为零或所有bn皆为零；

而且

等号仅当所有am皆为零时成立；类似地

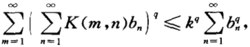
等号仅当所有bn皆为零时成立。

在上述式中，作为结论的三个不等式实际上是等价的，在最为重要的应用中，取K为

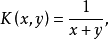即得定理1，这时，能满足(3)中的较强条件。

如果取K为

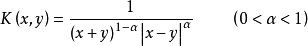则能满足(3)中的较弱条件。但这时需要用到条件(4)，以便将相等的对(m，m)从求和中去掉2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学