区域函数(region function)是一种以区域为自变量的函数,对任意的n∈N+,若D是Rn中的区域,而对D的每个子区域D′,对应着惟一的实数,这个对应关系(法则)F就称为定义在D上的一个区域函数。若对于D的任意两个没有公共内点的区域D₁和D₂,F还满足F(D₁∪D₂)=F(D₁)+F(D₂)(D₁∪D₂仍为区域时),则F可进一步称为加性区域函数,n=1时,(加性)区域函数可称为(加性)区间函数。数学分析中研究区域函数(区间函数)的意义在于,只有加性区域函数(区间函数),才可能用重积分或定积分表示。例如,面积、体积、位移、功等都是加性区域(区间)函数,因此,它们都能用重积分或定积分来进行计算;而像平均速度、平均密度、曲边梯形的平均高度这些物理量和几何量,则是没有加性的区域(区间)函数,所以,它们不可能表示成积分。在数学中,加性区域函数实质上是特殊的测度1。
基本介绍区域函数这个概念,是人们在实践活动中可以直接体验到的。例如,地球上区域的面积随着这个区域的不同而不同,又如非均匀金属丝的质量仍随着所取一段l的变化而变化,所以m就是l的函数,m=m(l)2。
定义 一般地,若变量u随着区域σ的变化而变化,我们就称u是区域σ的函数,记为

区域函数的导数—密度函数在引进二重积分时,讨论从物体的密度求质量的问题,这里要着重指出,物体的密度实际上是区域函数的某种导数,同一元函数的导数情形相似,利用极限可以从区域函数导出各种密度函数来2。
例如,当我们讨论非均匀细金属丝的质量分布时,为了刻划质量在各点的不均匀性,就要引进线密度概念。设细丝质量为m₁=m₁(l),它是线段l的函数,M是金属丝上的点,取含有点M的小段 ,
, 也用来表示这小段的长度,
也用来表示这小段的长度, 就是这一段细丝的平均密度;当
就是这一段细丝的平均密度;当 收缩到点M时,平均密度的极限值称为细丝在点M的线密度,记为μ₁(M),这是从区域函数m₁(l)诱导出来的点函数,也就是当
收缩到点M时,平均密度的极限值称为细丝在点M的线密度,记为μ₁(M),这是从区域函数m₁(l)诱导出来的点函数,也就是当 收缩到点M,因而
收缩到点M,因而 随着
随着 的消失而消失时所保留下来的关系。我们也记为μ₁(M)
的消失而消失时所保留下来的关系。我们也记为μ₁(M) ,随之有微分公式
,随之有微分公式

其中 是曲线(细丝)的弧长元素。
是曲线(细丝)的弧长元素。
一般地,设σ是空间Ω的区域,u(σ)是区域σ的函数,区域的度量(长度,面积或体积)仍记为σ,将σ无限细分,使得区域σ收缩到一点M,其度量σ→0,如果
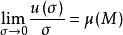 存在,则称μ(M)是u(σ)的密度,记为
存在,则称μ(M)是u(σ)的密度,记为 ,它是点M的函数,它的微分形式是
,它是点M的函数,它的微分形式是

例如,当σ是三维空间中的曲面时,μ(M)就是曲面的面密度,当σ是三维空间的物体时,μ(M)就是体密度。具体写出时,μ(M)都是x,y,z三元函数,但应该注意它们是从不同的区域函数导出的2。
密度函数的积分一元函数的微分和积分是高等数学中的一对基本矛盾,它们之间的对立统一,构成一元函数微积分学非常生动丰富的内容,这是辩证法在数学中的一个重要运用,相应地在多元函数的微积分中也是如此,上面已引进了各种区域函数的导数和微分的概念,得到区域函数u(σ)和密度函数μ(M)之间的关系: 。根据对立统一的观点,如果将
。根据对立统一的观点,如果将 在区域σ上重新无限累加起来,就得到积分:
在区域σ上重新无限累加起来,就得到积分: 。由于积分区域的不同,就有各种不同形式的积分;这些积分,无非是各种形式的区域函数罢了。下面分几方面来叙述2。
。由于积分区域的不同,就有各种不同形式的积分;这些积分,无非是各种形式的区域函数罢了。下面分几方面来叙述2。
1.直线上的线密度μ₁(x)和单积分
如果已知非均匀细杆的密度μ₁,求细杆的质量m,就是求积分
 其中
其中 .
.
2.平面上的面密度μ₂(x,y)和二重积分
如果已知薄片的密度μ₂(x,y),求薄片的质量,就是求二重积分
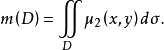
3.体密度μ₃(x,y,z)和三重积分
如果已知物体的密度μ₃(x,y,z),求这物体的质量,就是求三重积分

4.线密度和关于弧长元素ds的积分
空间曲线的弧长,也是由内接折线段长度之和的极限来表达,同平面曲线的情形相类似,空间曲线的弧长微分
 如果曲线的方程为
如果曲线的方程为 ,则
,则

曲线段的质量就是质量微元 的无限积累:
的无限积累:
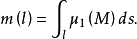 这种形式的积分称为函数μ₁(M)在曲线段l上关于弧长元素ds
这种形式的积分称为函数μ₁(M)在曲线段l上关于弧长元素ds
的积分。如果曲线的方程为 ,l的端点A,B所对应的参数为
,l的端点A,B所对应的参数为 ,那么这个积分可按下式计算2:
,那么这个积分可按下式计算2:
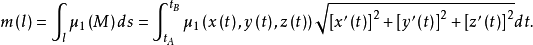
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国