[科普中国]-格雷果里级数

格雷果里级数(Gregory series)是反正切函数的幂级数展开式，由格雷果里(J.Gregory)于1671年得到，由于这个级数在计算π的历史中起过重大作用，故以格雷果里命名。

基本介绍格雷果里级数是反正切函数的幂级数展开式，由格雷果里(J.Gregory)于1671年得到

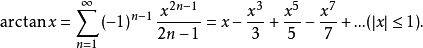由于这个级数在计算π的历史中起过重大作用，故以格雷果里命名。由此得到的

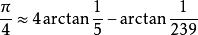称为梅钦公式。早在1706年，梅钦(J.Machin)用它计算π的值精确到了100位小数1。W.香克斯在1873年利用梅钦公式计算π值到707位小数，以后长期保持这个记录。但在1946年D.F.弗格森发现香克斯的第528位错了。他后来和美国J.W.小雷思在1948年联合发表808位准确的π值2。

相关介绍学过微积分的读者都知道近代计算π的准确数值的方法，就是利用收敛级数的算法。45度的角度等于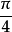 弧度。由麦克劳林定理可以得到所谓“格雷果里级数”：

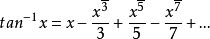
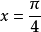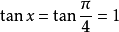的时候； ，所以

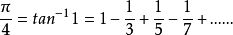利用这个级数就可以算出π的数值了。可惜这个级数收敛得很慢，用起来不方便。所以有人就利用

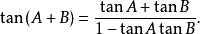这个三角关系式来得出

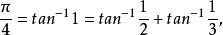
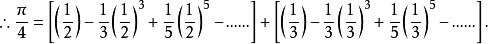我国清代曾纪鸿就利用这个式子计算π到100位3。

有人想出了收敛得更快的级数，如

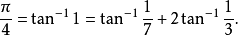1706年伦敦一位天文教授约翰·梅钦得出下列的式子：

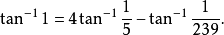1874年英国威廉·香克斯(1680-1751)i就利用这个式子用了十五年功夫计算π到707位小数。他这样做主要目的是要看π是不是一个循环小数，结果到了707位还看不出π是循环小数。1882年德国林德曼证明π是一个“超越数”，就是说π不可能是一个整系数代数方程式的根。超越数是无理数的一种。无理数不能以分数表示出来，只有分数才能以有限小数或循环小数表示出来。无理数以小数表示出来的时候，都是无限的不循环的小数3。

现在把π的真值头100位小数列出来、

π=3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679

要记住π的数值，在数种文字里都有些简短有趣的句子帮助我们记住它。如果只要四位小数，3.1416，在中文里有“山巅一狮一鹿。”在英文里有“Yes，I have a number。”Yes有三个字母，I一个，have四个，a一个，number六个。把字母的数目连起来正是3.14163。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学