[科普中国]-欧拉一麦克劳林公式

欧拉-麦克劳林公式(Euler-Maclaurin formula)是有关定积分的一种数值计算公式，它建立了函数的积分与其导数的联系。在数值积分理论与级数求和法中，Euler-Maclaurin公式是一个极有用的工具。

基本介绍欧拉-麦克劳林公式 设函数f(x)在区间[a,b]上有直到v阶连续微商，当v≥2时，给出欧拉-麦克劳林公式：

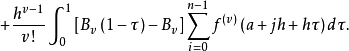这里 ，Bk是伯努利数，Bk(x)是伯努利多项式。可利用伯努利(Bernoulli)多项式的性质证明欧拉-麦克劳林公式。

相关说明下面对欧拉-麦克劳林公式作些说明1：

1．系数中用到的伯努利数和伯努利多项式都可由表查得，故此公式用起来很方便。

2．欧拉-麦克劳林公式可以被看作[a，b]上改善了的梯形公式，右端第二部分可看成修正项，最后那项看成余项。

3．欧拉-麦克劳林公式被应用时一般都取v为偶数，这是因为估计余项时使得余项里积分号下的因子 不变号的缘故。又因具奇标号的伯努利数等于零(除 外)。所以欧拉-麦克劳林公式可以写成

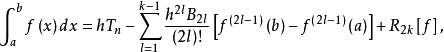其中

4．由于上面的余项表达式中包含有伯努利数，而伯努利数是随着k之增大而增大非常快的。故余项有时会趋向无穷。故使用这个公式时不应把k取得太大。一般用起来取2k=6，这时相应的伯努利数取最小值。又因余项里含有因子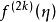也是使k不宜取得过大的原因1。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学