[科普中国]-数频连乘积定律

数频连乘积定律是一个科学问题，经典数学欧拉连乘积公式是一个不完备的表达式，这是两个形式极度相似而性质完全不同的领域，导致不同的结论科学完备与否。

简介数频连乘积定律是一个科学问题，经典数学欧拉连乘积公式是一个不完备的表达式，这是两个形式极度相似而性质完全不同的领域，导致不同的结论科学完备与否。

数频连乘积定律：。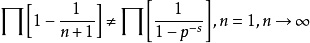

定律直接否定了欧拉的乘积，对于数频连乘积定律容易产生的误解是：将分子写成2·(2·2·2·3·2·4·2·5·6·......)然后对分母相互消去所有奇数，余下的部分2·2·.......2(2·4·6·8·.......)必然发散，从而得出欧拉乘积的悖论在于收敛和发散是有条件的，但一定不是等式。事实上分子分母项消去的只是无穷奇数的前一半所有项，而始终保留无穷奇数的后一半的无穷项。

欧拉连乘积公式欧拉常数最先由瑞士数学家莱昂哈德·欧拉(Leonhard Euler)在1735年发表的文章 De Progressionibus harmonicus observationes 中定义。欧拉曾经使用C作为它的符号，并计算出了它的前6位小数。1761年他又将该值计算到了16位小数。

欧拉自己的同一表达式却有两个不同的意义相反的结论，产生这种悖论就在于欧拉乘积不具有科学性。这种不完备在于省略了表达式的最后项，结果成了开放的级数。

意义数频连乘积定律取代欧拉连乘积的悖论，从而开启了21世纪的数频科学新领域。

在数频科学，否定欧拉乘积“定理”起于20世纪的哥德尔不完备定理；同样建立在等式基础上的数频科学连乘积定律也一并否定了哥德尔不完备定理。欧拉乘积“定理”经历了二百多年的研究与学习，在于它看似完整的论述，几乎天衣无缝地让人觉察不到它隐藏至深的悖论而深信不疑，这就注定了它一直在误导欧拉本人及其后来者的学术方向，注定了它是一个不断令人迷惑坠入不完备的深渊而不能自拔、没有希望的悖论，以此为基础而取得的看似连绵不断的辉煌学术“成果”，在数频科学诞生之日也就是它形神重新分合，各自成定律之时。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学