[科普中国]-欧拉链

若P为连通无向图G的一条链，G的每一条边在P中恰出现一次，则称P为欧拉链。

简介若P为连通无向图G的一条链，G的每一条边在P中恰出现一次，则称P为欧拉链。

若无向图G含有一条闭的欧拉链，则称图G为欧拉图。显然，一个图G若能一笔画出，这个图必然是欧拉图或含有欧拉链。1

定理①当且仅当连通图G的全部顶点都是偶次顶点时，图G才是欧拉图。

②当连通图G恰有两个奇次顶点时G才有欧拉链。

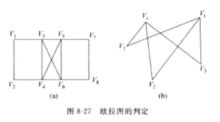
示例如图8-27(a)就是一个欧拉图，图8-27(b)就不是欧拉图，但有欧拉链{Vs,V1,Vs,V2,Vs,V3,V1}。

在图8—28(a)中，因所有顶点均为偶次，故是欧拉图。在图8—29(b)中，恰有两个奇次顶点，故有欧拉链。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学