[科普中国]-决策边界

在具有两个类的统计分类问题中，决策边界或决策表面是超曲面，其将基础向量空间划分为两个集合，一个集合。 分类器将决策边界一侧的所有点分类为属于一个类，而将另一侧的所有点分类为属于另一个类。

介绍决策边界是问题空间的区域，分类器的输出标签是模糊的。如果决策表面是超平面，那么分类问题是线性的，并且类是线性可分的。

决策界限并不总是明确的。 也就是说，从特征空间中的一个类到另一个类的过渡不是不连续的，而是渐进的。 这种效果在基于模糊逻辑的分类算法中很常见，其中一个类或另一个类的成员资格是不明确的。

在神经网络和支持向量模型中在基于反向传播的人工神经网络或感知器的情况下，网络可以学习的决策边界的类型由网络具有的隐藏层的数量来确定。如果它没有隐藏层，那么它只能学习线性问题。如果它有一个隐藏层，则它可以学习Rn的紧致子集上的任何连续函数1，如通用近似定理所示，因此它可以具有任意的决策边界。

特别地，支持向量机找到超平面，其将特征空间分成具有最大余量的两个类。如果问题最初不是线性可分的，则通过增加维数来使用内核技巧将其转换为线性可分的问题。因此，小尺寸空间中的一般超曲面在具有更大尺寸的空间中变成超平面。

神经网络试图学习决策边界，最小化经验误差，而支持向量机试图学习决策边界，最大化决策边界和数据点之间的经验边际。

线性可分集的决策边界与Logistuc Regression相比，SVM是一种优化的分类算法，其动机是寻找一个最佳的决策边界，使得从决策边界与各组数据之间存在margin，并且需要使各侧的margin最大化。比较容易理解的是，从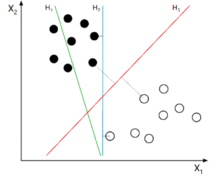决策边界到各个training example的距离越大，在分类操作的差错率就会越小。因此，SVM也叫作Large Margin Classifier。

最简单的情况是，在二维平面中的，线性可分情况，即我们的training set可以用一条直线来分割称为两个子集，如下图所示。而在图中我们可以看到，H2和H3都可以正确的将training set进行分类，但细细想来，使用H2进行分类的话，我们对于靠近蓝线的几个训练样例其实是不敢说100%的，但对于离蓝线最远的小球，我们却很有把握。这也是H3这条SVM红线出现的原因：尽量让两侧的训练样例远离决策边界，从而让我们的分类系统有把握对每个球Say Absolutely。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学