[科普中国]-自旋1/2

在量子物理中，自旋½表示一粒子所具有的内禀角动量（自旋）为ℏ/2，h是约化普朗克常数，其中包括了电子、质子、中子、中微子与夸克。自旋-½粒子在量子统计上属于费米子，并遵守泡利不相容原理。

简介在量子物理中，自旋½表示一粒子所具有的内禀角动量（自旋）为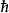，是约化普朗克常数，其中包括了电子、质子、中子、中微子与亏子(夸克)。自旋-½粒子在量子统计上属于费米子，并遵守泡利不相容原理。

对自旋½粒子进行自旋性质的量子测量会得到两个值。有两个结果肇因于所存有的矢量空间的维度。自旋½粒子的自旋量子态可以用一种两个维度的复数值矢量来描述，称之为二元旋量。利用这种表示法，量子力学中的算符可写成2乘2(2 x 2)的复数厄米矩阵。

自旋投影算符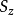意义上代表了沿着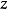方向对自旋做的测量：

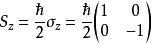
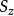算符有两个本征值——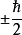，有各自对应的本征矢量：

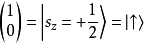
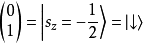其构成描述自旋之希尔伯特空间的完整基底，即自旋的态可用这两个态的线性组合来代表。这两个态方便上称之为“自旋向上”(spin up)与“自旋向下”(spin down)。

自旋算符S有些特质和角动量算符L相同，但其他特质则不相同。

可为自旋½物体建构升降算符；其遵守和其他角动量算符相同的对易关系(交换关系)。

自旋投影算符的旋转的两个本征值与前面相同(相应于测量的可能结果)，但本征矢量则不同——为矢量自旋算符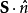；其中是一个顺沿投影方向的单位矢量，而

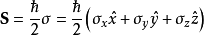
这些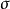为泡利矩阵或称泡利旋量。1

自旋-轨道作用在量子力学里，一个粒子因为自旋与轨道运动而产生的作用，称为自旋-轨道作用（英语：Spin–orbit interaction），也称作自旋-轨道效应或自旋-轨道耦合。最著名的例子是电子能级的位移。电子移动经过原子核的电场时，会产生电磁作用．电子的自旋与这电磁作用的耦合，形成了自旋-轨道作用。谱线分裂实验明显地侦测到电子能级的位移，证实了自旋-轨道作用理论的正确性。另外一个类似的例子是原子核壳层模型能级的位移。

半导体或其它新颖材料常常会涉及电子的自旋-轨道效应。自旋电子学专门研究与应用这方面的问题。2

参阅自旋-轨道作用

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学