[科普中国]-同伦切除定理

同伦切除定理是同伦论的一个重要定理。同伦群与同调群有很多相似的性质，如同伦型不变性、正合序列等，但是两者也有一些本质区别。

定理若(X;A,B,x0)是空间的三联组，使得(A,A∩B)是n连通的相对CW复形(n≥1)，(B,A∩B)是m连通的相对CW复形，则由包含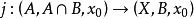映射诱导的映射对于1≤r≤m+n是同构，对于r=n+m是满同态。

意义同伦切除定理是同伦论的一个重要定理。同伦群与同调群有很多相似的性质，如同伦型不变性、正合序列等，但是两者也有一些本质区别。

例如，关于（奇异）同调群的切除性质对于同伦群来讲一般不成立。这也是使同伦群难以计算的重要原因之一。然而，通过对涉及的空间做一些限制，仍可以得到某种形式的切除性质。1

同伦论同伦论是拓扑学的重要概念。应该指出，映射的同伦关系是从拓扑空间X到Y的所有连续映射所成集合上的一个 等价关系，它将这些映射分成一些等价类，称每个等价类为一个同伦类。研究映射的同伦分类问题是同伦论的基本内容之一。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学