[科普中国]-多重复数

复数，为实数的延伸，它使任一多项式方程都有根，任一复数都可表达为x+yi，其中x及y皆为实数，分别称为复数之“实部”和“虚部”，多重复数的具体定义请参见正文。

简介在数学中，多重复数系Cn定义如下：令C0为实数系。F对每个n>0，令in为-1的平方根，然后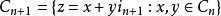。在多重复数系中还需要 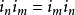(交换律)。

这样C1就是复数系，C2是双复数系，C3是科拉多塞格雷的三复数系，而Cn是n阶的多重复数。每个Cn形成一个巴拿赫代数。G. Bayley Price已写有关于多重复数的函数论，提供了双复数系C2的一些性质。多重复数系不能和克利福德代数混淆。因为克利福德代数里-1的平方根是反交换的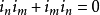（）。与子代数Ck的关系（k = 0, 1, ... n−1）：多重复数系Cn在Ck上的维数为2n-k。1

复数 (数学)复数，为实数的延伸，它使任一多项式方程都有根。复数当中有个“虚数单位”i，它是-1的一个平方根，即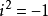。任一复数都可表达为x+yi，其中x及y皆为实数，分别称为复数之“实部”和“虚部”。

复数的发现源于三次方程的根的表达式。数学上，“复”字表明所讨论的数域为复数，如复矩阵、复变函数等。1

双复数双复数是拥有以下形式的超复数：

而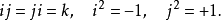

克利福德代数克利福德代数（Clifford algebra），又称几何代数（Geometric algebra），是综合了内积和外积两种运算，在几何和物理中在很多应用的一门数学学科。克利福德代数是复数、四元数和外代数的推广。

它的主要贡献者有：威廉·哈密顿（四元数），赫尔曼·格拉斯曼（外代数），威廉·金顿·克利福德，Hestenes等等，Hestenes是克利福德代数的发扬光大者。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学