[科普中国]-布劳威尔-加当-华定理

抽象代数中，布劳威耳-加当-华定理是个有关除环的定理，以德国数学家 Richard Brauer、法国数学家埃利·嘉当、以及中国数学家华罗庚命名。

简介抽象代数中，布劳威耳-加当-华定理是个有关除环的定理，以德国数学家 Richard Brauer、法国数学家埃利·嘉当、以及中国数学家华罗庚命名。

给定两个除环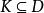使得对于所有D中非零的x都有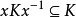（亦即，K的单位群是D的单位群的正规子群），则要么K被包含在D的中心，要么K=D。1

除环除环（division ring），又译反对称体（skew field），是一类特殊的环，在环内除法运算有效。需要特别注意的是，此环内必有非0元素，且环内所有的非0量都有对应的倒数（比如说，对于x来说，存在数a，使得 a·x = x·a = 1）。除环不一定是交换环，比如四元数环。

换种说法，一个环是除环当且仅当其可逆元群包含了环中所有的非零元素。

交换的除环就是域，因此我们只需研究非交换的除环。除四元数环外，如果把四元数环中的系数由实数改为有理数，则仍构成一个除环。更一般地，若R是一个环，S是R上的一个不可约模，则S的自同态环是一个除环。1

埃利·嘉当埃利·约瑟夫·嘉当（Élie Joseph Cartan，1869年4月9日─1951年5月6日），法国数学家，嘉当又译卡当、卡坦。他在李群理论及其几何应用方面奠定基础。他也对数学物理，微分几何、群论做出了重大贡献。1

单位群在环中，所有可逆元素叫环的单位，所有单位对乘法可构成一个乘法群，叫环的单位群。对环（域）来说，单位群所有元素，和环（域）的所有元素有多少相同，有多少不同，可由环的素理想，分式理想，理想类群来度量。

整数环Z的单位只有1，-1，单位群同构于循环群C2。模n 的剩余类环Zn单位群记为U（Zn）。仅有U（Z3），U（Z4），U（Z6），U（Z8），U（Z12），U（Z24）非单位元的阶均为2；非单位元的阶均为其他素数p（p > 2）的单位群不存在。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学