[科普中国]-西尔维斯特惯性定理

在代数学中，西尔维斯特惯性定理（Sylvester's law of inertia）是指在实数域中，一个二次型通过线性变换可以化简成唯一的标准型，具体定义请参加正文。

简介在代数学中，西尔维斯特惯性定理（Sylvester's law of inertia）是指在实数域中，一个形如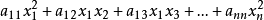的二次型通过线性变换可以化简成惟一的标准型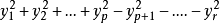。其中的正项数（称为正惯性系数）、负项数（称为负惯性系数）以及 0 的数目惟一确定，其中的r为系数矩阵的秩。正惯性系数p－负惯性系数的值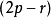称作符号差。1

线性映射在数学中，线性映射（有的书上将“线性变换”作为其同义词，有的则不然）是在两个向量空间（包括由函数构成的抽象的向量空间）之间的一种保持向量加法和标量乘法的特殊映射。线性映射从抽象代数角度看是向量空间的同态，从范畴论角度看是在给定的域上的向量空间所构成的范畴中的态射。

“线性算子”也是与“线性映射”有关的概念。但是不同数学书籍上对“线性算子”的定义存在区别。在泛函分析中，“线性算子”一般被当做“线性映射”的同义词。而有的书则将“线性算子”定义为“线性映射”的自同态子类。1

二次型在数学中，二次型是一些变量上的二次齐次多项式。例如

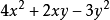是关于变量x和y的二次型。

二次型在许多数学分支，包括数论、线性代数、群论(正交群)、微分几何(黎曼测度)、微分拓扑(intersection forms of four-manifolds)和李代数(基灵型)中，占有核心地位。1

参见二次形式 (统计)

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学