[科普中国]-广义剩余定理

广义剩余定理亦称广义贝祖定理，是余数定理在矩阵多项式上的推广。

简介广义剩余定理亦称广义贝祖定理，是余数定理在矩阵多项式上的推广。

给定数域P上的矩阵多项式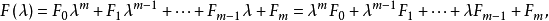 其中F0，F1，...，Fm为P上的n阶矩阵，且F0≠0，则以λE-A右除F(λ)所得的余式为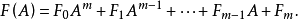以λE-A左除F(λ)所得的余式为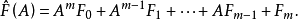

λE-A右（左）整除矩阵多项式F(λ)的充分必要条件是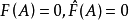：。1

余数定理（Polynomial remainder theorem）

余数定理是指一个多项式f(x) 除以一个线性多项式(x-a)的余数是 f(a)。若f(a)=0，则(x-a)为多项式f(x)的因式。例如，(5x³+4x²-12x+1)/(x-3) 的余式是 5·3³+4·3²-12·3+1=136。

矩阵多项式(matrical polynomial)

矩阵多项式是一种特殊矩阵。设A0，A1，…，As是数域P上的m×n矩阵，λ是一个文字，则A0λs+A1λs-1+…+As-1λ+As称为矩阵多项式。

矩阵多项式涉及有矩阵多项式的运算、矩阵多项式的右（左）除。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学