[科普中国]-两元素布尔代数

两元素布尔代数是最简单的布尔代数，它只有两个元素，习惯指名为 1 和 0。保罗·哈尔莫斯给这个起名为 2，被一些文献和本文采用。

简介两元素布尔代数是最简单的布尔代数，它只有两个元素，习惯指名为 1 和 0。保罗·哈尔莫斯给这个起名为2，被一些文献和本文采用。

任何布尔代数都关联着叫做“全集”或“载体”的一个偏序集合B，使得这个布尔代数的运算是从Bn到B的映射。这个载体是由于有显著的成员 0 和 1 而是有界的。2简单的就是其载体同一于它的界的集合的布尔代数，即B={0,1}。

布尔代数的两个二元运算有很多名字和符号。这里把它们叫做“和”与“积”，分别符号表示为中缀 + 和。积经常指示为两个操作数的简单串联。和与积是交换的和结合的，如同普通的实数代数中那样。在运算次序上，优先于 + 但是括号可以超越它。所以“AB+C”被分析为“(AB)+C”而非“A(B+C)”。

一元运算总是被称为“补”，这里的符号表示是对参数放置上横杠。x的补的数值类似者是 1-x。在泛代数的语言中，所有布尔代数是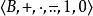代数，型为。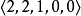

解释 0 和 1 中的一个为“真”另一个为“假”产生了经典的等式形式的二值逻辑。在这种情况下，+ 被读做或，被读做与，而补被读做非。1

布尔代数在抽象代数中，布尔代数(英语：Boolean algebra)是捕获了集合运算和逻辑运算二者的根本性质的一个代数结构（就是说一组元素和服从定义的公理的在这些元素上运算）。特别是，它处理集合运算交集、并集、补集；和逻辑运算与、或、非。1

逻辑代数在数学和数理逻辑中，逻辑代数（有时也称开关代数、布尔代数）是变量的值仅为真和假两种真值（通常记作 1 和 0）的代数的子领域。初等代数中变量的值是数字，并且主要运算是加法和乘法，而逻辑代数的主要运算有合取与，记为∧；析取或，记为∨；否定非，记为¬ 。因此，它是以普通代数描述数字关系相同的方式来描述逻辑关系的形式主义。

逻辑代数是乔治·布尔（George Boole）在他的第一本书《逻辑的数学分析》（1847年）中引入的，并在他的《思想规律的研究》（1854年）中更充分的提出了逻辑代数。根据Huntington“布尔代数”这个术语，最初是由Sheffer于1913年提出。

逻辑代数一直是数字电路设计的基础，并且所有现代编程语言提供支持。它也用在集合论和统计学中。1

参见逻辑代数

卡诺图

Quine-McCluskey算法

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学