[科普中国]-欧德里兹科-肖恩哈格算法

在数学中，欧德里兹科-肖恩哈格算法是一个用于评估多点上黎曼ζ函数的值的快速算法，由(Odlyzko & Schönhage 1988)发现。

简介在数学中，欧德里兹科-肖恩哈格算法是一个用于评估多点上黎曼ζ函数的值的快速算法，由(Odlyzko&Schönhage1988)发现。其主要思想是使用快速傅里叶变换加速N个等O(N)间隔的值的有限狄利克雷级数的计算，从O(N2)步减少到O(N1+ε)步（花费存储O(N1+ε)个中间值的代价）。黎曼-西格尔公式，用于计算虚部为T点上黎曼ζ函数的值，使用约N=T1/2项的有限狄利克雷级数，所以要找到N个黎曼ζ函数的值时，它将加速约T1/2倍。这将找到虚部不超过T的ζ函数零点所需的时间从大约T3/2+ε步减少到了大约T1+ε步。

该算法不仅可以用于黎曼ζ函数，还可以用于狄利克雷级数给出的许多其他函数。该算法被Gourdon (2004)用于验证黎曼猜想ζ函数的前10个零点。1

黎曼ζ函数黎曼ζ函数ζ（s）的定义如下： 设一复数s，其实数部分> 1而且：

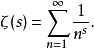它亦可以用积分定义：

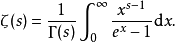
在区域{s: Re(s) > 1}上，此无穷级数收敛并为一全纯函数（其中Re表示复数的实部，下同）。欧拉在1740考虑过s为正整数的情况，后来切比雪夫拓展到s>1。波恩哈德·黎曼认识到：ζ函数可以通过解析开拓来扩展到一个定义在复数域（s,s≠ 1）上的全纯函数ζ（s）。这也是黎曼猜想所研究的函数。

虽然黎曼的ζ函数被数学家认为主要和“最纯”的数学领域数论相关，它也出现在应用统计学（参看齐夫定律（Zipf's Law）和齐夫-曼德尔布罗特定律（Zipf-Mandelbrot Law））、物理，以及调音的数学理论中。1

黎曼猜想黎曼猜想由德国数学家波恩哈德·黎曼（Bernhard Riemann）于1859年提出。它是数学中一个重要而又著名的未解决的问题（猜想界皇冠）。多年来它吸引了许多出色的数学家为之绞尽脑汁。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学