[科普中国]-皮利福梅曲线

皮利福梅曲线(Piriforme curve)是一种由圆产生的曲线，己知圆x²+y²-ax=0上一动点Q，过Q与x轴平行的直线交圆之定直径DD(x=a)于K。过原点O与K的连线交过Q而与y轴平行的直线于P点，则P点的轨迹称为“皮利福梅曲线”。它的方程是：x4-2ax³+a²y²=0，参数方程为：x=a(1+cosθ);y=asinθ(1+cosθ)1。

基本介绍皮利福梅曲线是一种由圆产生的曲线，过圆x²+y²-2ax=0(a>0)上的动点P与x轴平行的直线交圆之定直径AB(x=a)于Q，直线OQ与过点P且平行于y轴的直线的交点M的轨迹(见图)称为皮利福梅曲线。

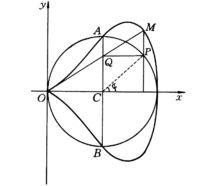
皮利福梅曲线的方程皮利福梅曲线所围的面积为πa²。它的直角坐标方程为x4-2ax³+a²y²=0；参数方程为

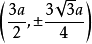其中φ=∠xCP，极值点坐标，拐点坐标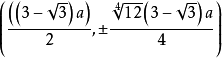，尖点坐标(0，0)2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学