[科普中国]-平面仿射坐标

平面仿射坐标(affine coordinates in plane)是一种平面坐标，平面上取两条相交的轴x与y，交点O称为原点，在两轴上各取一个单位点E₁，E₂，使x轴和y轴都成为坐标轴，对于平面上的任意点M，过M作两轴的平行线，设它们与轴x，y的交点分别为M₁，M₂，它们在轴x，y上的坐标分别为x，y，因而点M对应着有序实数对(x，y)，反过来，任意给一有序实数对(x，y)，可以分别在x，y轴上作出坐标为x，y的点M₁，M₂，过M₁，M₂分别作y轴、x轴的平行线，得到其交点M，可见平面上所有点与全体有序实数对(x，y)之间存在一一对应关系，这个一一对应关系称为平面仿射坐标系，又称平行坐标系，有序实数对(x，y)称为点M的平面仿射坐标，x，y分别称为点M的第一坐标和第二坐标。平面仿射坐标系的两轴上，长度单位一般不同，如果相同就是斜坐标系，两轴的夹角可为任意角，若等于直角，且两轴上的长度单位相同，则为直角坐标系。

平面仿射坐标系在平面解析几何中，通过在平面上建立直角坐标系或极坐标系，把平面上的点与一对有次序的数对应起来，把平面上的图形与二元方程对应起来，从而用代数方法来研究平面几何问题。需要指出的是，建立平面上的点与一对有次序的数之间的对应关系并不限于直角坐标系或极坐标系。还有另一种更为一般的坐标系——仿射坐标系。

在平面上取定一点O和两个以点O为起点的不共线向量e₁，e₂，称为平面上的一个仿射坐标系，记作{0；e₁，e₂}。其中O称为原点，e₁，e₂称为基向量(简称基)或坐标向量。若e₁，e₂符合右手规则，则称此坐标系为右手系，否则称为左手系。如不特别声明，一般指右手系。过O点且分别平行于e₁，e₂的有向直线(它的正向与基向量的方向相同)称为坐标轴。共有两条坐标轴，依次称为x轴和Y轴。两条坐标轴分平面为四部分，依次称为第Ⅰ，Ⅱ，Ⅲ，Ⅳ象限(图1)。

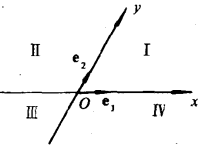
若仿射坐标系{0；e₁，e₂}的基向量e₁，e₂互相垂直，且|e₁|=|e₂|=1，就成为平面直角坐标系。可见，平面直角坐标系是平面仿射坐标系的特殊情形1。

平面上点的仿射坐标在平面仿射坐标系{0；e₁，e₂}中给定一点M，就确定唯一的向量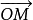 ，称为点M的向径。向径 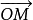可唯一地表示成

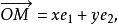
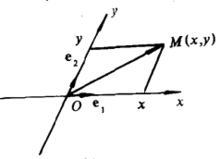
如图2所示。由此可见，向径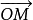 与有序数组(x，y)之间建立了一一对应关系。有序数组(x，y)称为向径 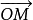在仿射坐标系{0；e₁，e₂}下的坐标，也称为点M在仿射坐标系{0；e₁，e₂}下的坐标，记作M(x，y}1。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学