[科普中国]-加速骚扰

加速骚扰也称为加速扰动或加速摄动，摄动理论是使用一些特别的数学方法来对于很多不具精确解的问题给出近似解，这些方法从相关的较简单问题的精确解开始入手。摄动理论将原本问题分为具有精确解的较简单部分与不具精确解的微扰部分。摄动理论适用的问题通常具有以下性质：通过加入一个微扰项于较简单部分的数学表述，可以计算出整个问题的近似解。

简介加速扰动理论使用一些特别的数学方法来对于很多不具精确解的问题给出近似解，这些方法从相关的较简单问题的精确解开始入手。加速扰动理论将原本问题分为具有精确解的较简单部分与不具精确解的微扰部分。加速扰动理论适用的问题通常具有以下性质：通过加入一个微扰项于较简单部分的数学表述，可以计算出整个问题的近似解。

加速扰动理论计算出来的解答通常会表达为一个微小参数的幂级数。加速扰动理论解答与精确解之间的差别，可以用这微小参数来做数量比较。幂级数的第一个项目是精确解的解答。后面的项目描述解答的修正。这修正是因为精确解与原本问题的“完全解”之间的误差而产生的。更正式地，完全解的近似可以表达为一个级数：1

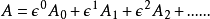
在这例子里，A0是简单又有“精确解”的问题的精确解，A1,A2......代表由某种系统程序反复地找到的高阶项目修正。因为的值很微小，这些高阶项目修正应该会越来越不重要。

微扰阶数加速扰动理论的标准阐述主要是以微扰的阶数来分辨：一阶加速扰动理论或二阶加速扰动理论。再来就是以微扰的简并度来分辨：无简并或有简并。有简并的摄动，又称为奇异摄动（singular perturbation），比较难解，必须用到更进阶的理论。2

本词条内容贡献者为:

李航 - 副教授 - 西南大学