[科普中国]-二次曲线族

二次曲线族是二次曲线的集合，指具有某种共同性质的二次曲线的全体，它可简化求适合一定条件的二次曲线的方程的步骤，随着独立参数个数的不同，把二次曲线族按其参数的个数而分为单参数二次曲线族、双参数二次曲线族等。

基本概念在二次曲线的方程

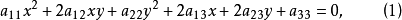中，二次项的系数不全为零，不妨设a11≠0,那么以a11除方程两边，所得到的方程

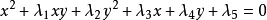仍然表示同一条曲线，这个方程中含有五个独立的系数(亦称参数)，如果给这些参数各种不同的数值，可得到各种不同的曲线，形成一族二次曲线，称它为二次曲线族。又随着独立参数个数的不同，把二次曲线族按其参数的个数而分为单参数二次曲线族、双参数二次曲线族等。例如:

如果二次方程(1)的参数满足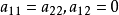，那么这二次方程所含的独立参数的个数就由五个减到三个而成为三参数二次曲线族，即圆族。

如果二次方程(1)的参数满足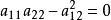 ,那么这二次方程所含的独立参数的个数就由五个减到四个而成为四参数二次曲线族，即抛物线族。

如果二次方程(1)的参数满足 ,那么这二次方程所含的独立参数的个数并没有减少，仍为五个独立参数，是五参数二次曲线族，即中心二次曲线族。

二次曲线族可简化求适合一定条件的二次曲线的方程的步骤：

1.给定两条二次曲线F1(x，y)=0，F2(x，y)=0，经过这两条二次曲线的所有交点(一般有4个)的二次曲线族的方程为λ1F1(x，y)+λ2F2(x，y)=0，式中λ1，λ2是不同时为零的参数。

2.经过两条直线Li=Aix+Biy+Ci=0(i=1，2)与二次曲线F(x，y)=0的交点的二次曲线族的方程为F(x，y)+λL1L2=0，式中λ是参数。

3.经过4点Pi(xi，yi)(i=1，2，3，4)的二次曲线族的方程为L12L34+λL23L41=0，式中λ是参数，Li，i+1=(yi+1-yi)(x-xi)-(xi+1-xi)(y-yi)，x5=x1，y5=y1。

4.与已知两直线L1=0，L2=0分别相切于已知点P1(x1，y1)，P2(x2，y2)的二次曲线族的方程为L²12+λL1L2=0，式中L12=(y2-y1)(x-x1)-(x2-x1)(y-y1)，λ是参数，例如，已知A(-1，0)，B(1，0)，C(a，b)和AB边上的中线OC上一点P，OP/OC=f，则与两直线AC，BC分别相切于点A，B，且过点P的二次曲线为f²b²x²-2f²abxy+(f²a²+1-2f)y²+2f²by-f²b²=0，当f=1/2时，图形为抛物线；当0