[科普中国]-莱克塞尔定理

莱克塞尔定理(Lexell theorem)是关于球面上点的轨迹的一个定理。.该定理断言：若给定球面三角形的两个顶点及面积，则第三个顶点的轨迹是两个小圆，它们通过两已知顶点的对径点，莱克塞尔(А.И.Лекселъ)在球面三角、球面几何方面发表过四卷集的专著，此定理为他首先证明1。

基本介绍莱克塞尔(Lexl)定理 设给定球面三角形的面积和两个顶点，则第三个顶点的轨迹由两个小圆组成，这两圆通过两已知顶点的对径点。

莱克塞尔(Lexl)定理的证明介于相交的两个半大圆之间的球面部分，称为球面月形，换言之，即球面被以一直径为棱的二面角所截的部分。这两半大圆的交角，即这二面角的度量，称为月形的角(下图)，于是有2

定理1 同球两月形之比等于它们的角之比。

注意：

1.角相等的两个月形角是全等的，因为迭合了它们相应的二面角，它们便迭合了。

2.以两月形A, B的角之和为角的月形C,其面积为A, B面积之和，只要使两月形成为相邻的，就显然了(下图)，而由1，我们是可以这样办的。

从上面所指出的两点，可以推出我们想要证明的命题。

系 月形的面积是它的角的两倍(在所设的单位制下)。

因为角为直角的月形显然是球面的四分之一，因此它的面积是数π，至于它的角则为π/2。

由于这个月形面积的度量与角的度量之比等于2，所以对于一切其他月形也如此2。

引理两个互相对称的球面三角形是等积的。

定理2球面三角形的面积是它的角的和与π的差。

证明 设ABC是所考虑的三角形，A',B' ,C'是A,B,C的对径点(图1)，以三角形ABC的∠A为角的月形，由三角形ABC加上三角形BCA'所组成，即：

月形∠A=△ABC+△BCA'，

同理：

月形∠B=△ABC+△ACB'，

月形∠C=△ABC+△ABC'。

但在最后的等式中,三角形ABC'可以用它的等积三角形A'B'C'来代替（上述定理），于是将三等式相加，并注意三角形ABC, BCA' , CAB' ,A'B'C之和，就是被大圆AB所决定的丙半球之一，因而以2π为度量，便得

月形∠A+月形∠B+月形∠C=2△ABC+2π；

由于月形∠A =2∠A，月形∠B=2∠B，月形∠C=2∠C，所以

△ABC=∠A+∠B+∠C-π。

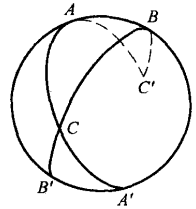
莱克塞尔(Lexl)定理的证明 设C(图1)为动顶点，A,B为已知点，A',B’为A,B的对径点，我们知道了三角形ABC三角的和，但三角形A'B'C的∠CA'B'和∠CB'A'分别等于∠CAB'和∠CBA'，即等于∠A和∠B的补角，因此，和∠A+∠B+∠C可写作∠C+2π-∠CA'B' -∠CB'A'，所以我们知道了∠CA'B' +∠CB'A'-∠C，于是点C的轨迹由通过A'，B'的两小圆组成2。

球面四边形的Lexell定理球面四边形的Lexell定理(Lexell’S theorem for a sphericalquadrilateral)：

球面四边形ABCD内接于小圆的充分必要条件是：∠A+∠C=∠B+∠D。

本题选自Lexell，Acta petropolitana(1782)。

Lexell是俄国数学家莱克塞尔(А.И.Лекселъ，1740~1784)，在球面三角、球面几何方面发表过四卷集的专著。例如，他给出了如下定理：若给定球面三角形的两个顶点及面积，则第三顶点的轨迹是两个小圆，它们通过已知顶点的对径点。

与平面几何对照，这个定理与平面上四点共圆定理相仿，若令球面半径趋于无穷大，球面四边形的角盈趋于零，则该定理即演化为平面上的四点共圆定理3。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学