[科普中国]-双曲型反演变换

双曲型反演变换是反演变换的一种，指反演幂k>0的反演变换，这时k可表为k=r2(r>0)，r称为反演半径，通常称双曲型反演变换为关于反演基圆（球）的反演变换。

公式简介双曲型反演变换是反演变换的一种，指反演幂k>0的反演变换，这时k可表为k=r2(r>0)，r称为反演半径。1

反演基圆以反演中心O为圆（球）心，以反演半径r为半径作圆（球），根据反演变换的定义，此圆（球）上的点的反演点是它自身，这样的点称为反演变换的二重点，并将此圆（球）称为反演基圆（球）。由于这个圆的存在，因而通常称双曲型反演变换为关于反演基圆（球）的反演变换。

只要给定反演中心O和反演幂k>0，这个双曲反演变换就是确定的，因而对于平面上（空间中）的非反演中心的任意一点A，都可利用几何作图求出其反演点A'。

求反演点求反演点的方法：

首先以O为圆心，以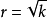为半径作反演基圆。

1.若A点在⊙O(r)上，则点A'与点A重合（如图1）。

2.若A点在⊙O(r)外，从A点向⊙O(r)作一条切线，切点为P，从P点引OA的垂线，垂足即为A'（如图2）。

3.若B点在⊙O(r)内，则与2的作图相反，即过B点作OB的垂线交⊙O(r)于点P，过P点作⊙O(r)的切线交OB的延长线于B'点，B'即为B的反演点（如图2）。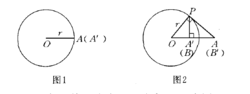

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学