卷积模型可以用来模拟某些图像变换,但由于其仅仅是对图像落入卷积核支撑域的各个局部进行的凸线性变换,限制了它的适用范围。基于此,我们提出了非线性卷积过程。
两种广义的非线性卷积高阶卷积高阶卷积在运算中除了考虑图像的一阶变换,还引入了更高阶变换,用以扩展卷积模型的拟合范围,其过程可以表达为 ,然而,过高的阶数会造成计算的不稳定和低效,因此一般用到2阶信息,即高阶卷积核为
,然而,过高的阶数会造成计算的不稳定和低效,因此一般用到2阶信息,即高阶卷积核为 。
。
置换卷积置换卷积.一般卷积变换都具有空间位移不变性,即变换仅发生在亮度空间而不改变空间位置,因此它们所模拟的图像风格必须满足坐标对齐性质。置换卷积定义为不改变图像的亮度而仅仅改变像素位置。置换卷积核中每个元素为一置换向量,通过该向量将像素坐标映射到新的位置.具体表示为

对于大多数的图像过程,置换向量都不是固定常量,而是一个随机向量,因此需要计算置换向量的平均值来确定置换卷积核 1。
1。
卷积核的估计高阶核估计高阶卷积核是普通卷积核的推广,因此其估计算法也与一般核估计算法相近。高阶卷积过程为 ,对于训练集合A和A'来说,,将其展成向量形式为
,对于训练集合A和A'来说,,将其展成向量形式为 。此问题是一个典型的过静定问题,最简便的解法是最小二乘法。为增强稳定性,利用Tikhonov正则化将其变为最小化问题
。此问题是一个典型的过静定问题,最简便的解法是最小二乘法。为增强稳定性,利用Tikhonov正则化将其变为最小化问题
 其中设定
其中设定 ,该优化问题在全局空间的解为
,该优化问题在全局空间的解为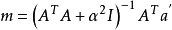 。推广到2阶空间,并要求m1非负,在这些约束下,最佳解可以采用迭代计算方式求出:
。推广到2阶空间,并要求m1非负,在这些约束下,最佳解可以采用迭代计算方式求出:
step1.初始化: ;
;
step2.计算
step3.扫描 ,若
,若 ,则令
,则令 =0
=0
step4.重新正则化,
其中 是调节因子,可以调控收敛速度,一般取
是调节因子,可以调控收敛速度,一般取 =0.5..当迭代的相邻误差较小时,就可以终止迭代, 输出结果1。
=0.5..当迭代的相邻误差较小时,就可以终止迭代, 输出结果1。
置换核估计由于置换作用仅仅改变像素位置,因此可以采用搜索的办法估计置换核在搜索域内为每个像素寻找置换向量,搜索域分为初始域G和置换域Gm.设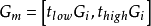 ,其中
,其中 和
和 分别是内外比例限参数,取
分别是内外比例限参数,取 =05,
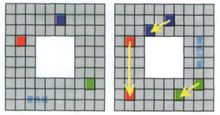
=05, =2。在Gm中以栅格顺序进行匹配搜索,匹配距离定义为色彩空间的欧氏距离.如图1所示,由于图像的亮度信号重要性远远超过色差信号,为了加快搜索计算速度,我们用和文献7中同样的思路,将RGB图像变换至YUV空间,并在Y空间计算匹配距离。
=2。在Gm中以栅格顺序进行匹配搜索,匹配距离定义为色彩空间的欧氏距离.如图1所示,由于图像的亮度信号重要性远远超过色差信号,为了加快搜索计算速度,我们用和文献7中同样的思路,将RGB图像变换至YUV空间,并在Y空间计算匹配距离。
具体地,对 ,设其匹配集合为
,设其匹配集合为 ,将各个匹配集合中所有数据均引入置换向量库,得到最后的统计样本
,将各个匹配集合中所有数据均引入置换向量库,得到最后的统计样本 ;则置换核为
;则置换核为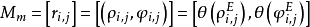 ,其中
,其中 是数学期望。
是数学期望。
.高阶核估计的前提是没有显著的置换发生; 而置换核计算的前提正好相反,两者相互对立,要确定完整的卷积模型必须解决这个矛盾,可以采用多分辨率方式加以处理1。
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国