[科普中国]-数据依赖

数据依赖，数学概念，是通过一个关系中属性间值的相等与否体现出来的数据间的相互关系，数据依赖是现实世界属性间相互联系的抽象，属于数据内在的性质。在计算机科学中，数据依赖是指一种状态，当程序结构导致数据引用之前处理过的数据时的状态。在编译学中，数据依赖是数据分析的一部分。

数学定义定义：设有一关系模式R（A1,A2,…,An),X和Y均为（A1,A2,…,An)的子集，对于R的值r来说，当其中任意两个元组u,v中对应于X的那些属性分量的值均相等时，则有u,v中对应于Y的那些属性分量的值也相等，称X函数决定Y，或Y依赖于X，记为X->Y1。

例：有关系，学生（学号S#，姓名SN，系名SD），子集X（学号S#），子集Y（系名SD）。

每个学生有唯一的一个学号，学生中可以有重名的姓名，每个学生只能属于一个系，每个系有唯一的系代号。有此，可以找出学生关系模式中存在下列函数依赖：

S#->SN；S#->SD

例：有关系，学校简况(学号S#，系名SD，系主任MN，课程CN，成绩G)。可写出函数依赖：

S#->SD；SD->MN；S#,CN->G

根据函数依赖的不同性质，函数依赖可分为完全函数依赖、部分函数依赖和传递函数依赖。

2.2 完全函数依赖

定义：在R(U)中，如果X->Y，对于X的任意一个真子集X’,都有X’不能决定Y，则称Y对X完全函数依赖，记为XY 。

例：（S#,CN）->G

2.3 部分函数依赖

定义：在R(U)中，如果X-> Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖。

2.4 传递函数依赖

定义：在R(U)中，当且仅当X-> Y，Y->Z时，称Z对X传递函数依赖。

例：描述学生（S#）、班级（SB）、辅导员（TN）的关系U(S#,SB,TN)。一个班有若干学生，一个学生只属于一个班，一个班只有一个辅导员，但一个辅导员负责几个班。根据现实世界可得到一组函数依赖：

F={S#->SB，SB->TN}

学生学号决定了所在班级，所在班级决定了辅导员，所以辅导员TN传递函数依赖于学生学号S#。

数据依赖还包括多值依赖和连接依赖两种形式。

--------------------------------------------------------------------------------------------------

计算机学定义数据依赖是指一种状态，当程序结构导致数据引用之前处理过的数据时的状态。在编译学中，数据依赖是数据分析的一部分。

解说：假设有如下表述S1和S2，

(I (S1) ∩ O(S2)) ∪ (O(S1) ∩ I(S2)) ∪ (O(S1) ∩ O(S2)) ≠ Φ

那么S2依赖S1。I（Si）是内存位置的集合，可由Si和S2读

O（Sj）是内存地址的集合，由Sj写，

则这里S1和S2就有一个必须遵守的执行顺序。

种类数据依赖有三种，

1. 流依赖（flow dependency)，一个变量在一次表达式中赋值或修改然后用在后来的另一个表达式中。例

a=b*c

...

d=a-e

2.反依赖（anti dependency)，一个变量在一个表达式中被使用然后在后来一个表达式中被修改赋值。例

a=b*c

......

b=d+e

3.输出依赖，一个变量在一表达式中被修改赋值然后又在后来另一个表达式中被修改值，例

a=b+c

......a=d-e

数据库中的数据依赖数据依赖是数据之间的相互制约关系，是一种语义体现，主要分为函数依赖（FD）、多值依赖（MVD）和连接依赖（JD）2。

函数依赖两个实例化的属性集X,Y，如果属性集X中的两个元组取值相同，必有对应的另外一个属性集Y中元组取值相同，则称Y函数依赖于X函数。

特别值得注意的是，如果属性集X中不存在两个取值相同的元组集合，则Y必定依赖于函数X，且函数X的属性集为超键。

平凡函数依赖和非平凡函数依赖。平凡函数依赖：如果Y依赖于X，同时Y是X的子集，那么称X -> Y 为平凡函数依赖；非平凡函数依赖：Y不是X的子集。对于任意关系模式而言，平凡函数依赖是必然成立的，其并不反映新的语义特征，因此我们一般不讨论平凡函数依赖。

完全函数依赖和部分函数依赖。完全函数依赖表示的就是函数X的属性集构成了候选键。其中形式化的表示就是如果对于X的任何一个子集Z，都有Y不依赖于X，则称Y完全函数依赖于X。如果Y不完全函数依赖于X，则称Y部分函数依赖于X。完全函数依赖的左部构成主键，不包含冗余的属性。

传递函数依赖和直接函数依赖。如果Y函数依赖于X，Z函数依赖于Y，其Y不是X的子集，X不依赖于Y，则称Z传递依赖于X，否则称Z直接函数依赖于X。

函数依赖的逻辑蕴涵。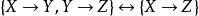 ，即对于关系模式上的函数依赖集合F，只要X→Y是一个函数依赖，那么必然可以推导认为F逻辑蕴涵X→Y。

函数依赖集合的闭包。由函数依赖集合F所逻辑蕴涵的全部函数依赖所构成的集合称之为F的闭包。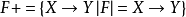 。闭包的性质：1. F 属于 F+，这是因为根据闭包的定义F中的每个函数依赖必定也在中F+；2. (F+)+=F+，该性质说明闭包运算是幂等的，即F经过任意多次的闭包运算后其结果仍然等于F+；3.如果F=F+，则称F是完备的。

函数依赖的推理规则（Armstrong公理）：

设U是关系模式R的属性集，F是R上的函数依赖集，则有：
A1（自反律）：如果Y X U，则X→Y成立；
A2（增广律）：如果X→Y成立，且Z U，则XZ→YZ成立；
A3（传递律）：如果X→Y，Y→Z成立，则X→Z成立。

多值依赖定义：对于某个关系上的三个属性A, B, C。如果属性B，C的取值都不单一，同时B的取值与C无关，也就是B依赖于A，随着A取值的变化可以取不同的值。

形式化描述：设R(U)是属性集U上的一个关系模式。X，Y，Z是的U的子集,并且Z=U-X-Y，如果对R(U)的任一关系r，都有如下性质：如果r中存在2个元组s、t，使得：s[X]=t[X] ，则r中必存在元组u，使得： (1) s[X]=t[X]=u[X] (2) u[Y]=t[Y] 且 u[Z]=s[Z] (即交换s、t在Y上的值得到的2个元组必在r中) 则称关系模式R满足多值依赖X→→Y。

注意事项：多值依赖会导致数据冗余和更新异常，因此在进行数据模式设计的时候，要消除多值依赖。一般使用的方法是建立两个关系，让每个关系只存储一个多值属性的数据。

推导规则：

A4：互补律(MVD) 如果X→→Y，则X→→(U-XY)
A5：扩展律(MVD) 如果X→→Y且VW，则WX→→VY
A6：传递律(MVD) 如果X→→Y且Y→→Z，则X→→(Z-Y)
下面两条为(FD+MVD)公理：
A7：如果X→Y，则X→→Y，即FD是MVD的特例
A8：如果X→→Y、Z→→Y且对某个与Y不相交的W有：W→Z，则X→Z

连接依赖设关系模式R、Ri的属性集是U、Ui，UiU(1≤i≤n).若R每个容许的实例r均满足r=∏U1(r)∞...∞∏Un(r)则称R满足连接依赖，记作∞(R1,...,Rn).若其中某个Ui=U，则称连接依赖是平凡连接依赖。 多值依赖也是连接依赖。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学