[科普中国]-巴哈杜尔有效性

巴哈杜尔(Bahadur)1960年提出的一种估计量渐近有效性的概念。设总体X的概率函数p(x;θ)依赖于m维未知参数θ=(θ1，…，θm)，θi(i=1，…，m)是θi的相合估计量， 基于容量为n的简单随机样本，θ(n)=(θ1，…，θm); 记D (θ) 是以∂lnp(X;θ)/∂θi(i=1，…，m)为分量的m维列向量，D′(θ)是D(θ) 的转置 (m维行向量)，I(θ) =E[D(θ) D′(θ)] 。称θ(n)为θ的巴哈杜尔渐近有效估计量。

对相合估计给出了大偏差的渐近下界，达到这一下界的估计称为Bahadur渐近有效的。

巴哈杜尔渐近有效性的定义中，除要求估计量具有相合性之外，再无其他更多的限制，因此应用较广。但是其比较的标准不够直观且比较粗糙。

定义设X1，……，Xn为iid样本，抽自总体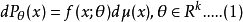 当分布族(l)满足具有共同支撑集等正则条件时，则对任一具有连续偏导数的向量函数g(θ)=()'，（r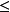k），其任一相合估计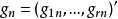必有

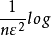
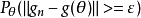
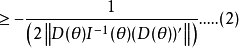
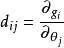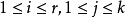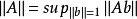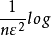
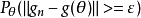
其中I(θ)是总体（1）的Fisher信息阵，，，。模||.||定义为：当a为向量时，||a||是欧氏模，而当A是方阵时，。因此，当估计量gn满足条件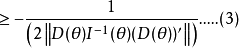时，称其为Bahadur渐近有效估计。这种渐近有效性是Bahadur提出的。

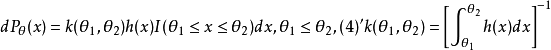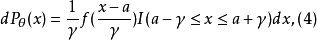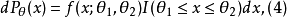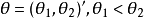但是对非正则条件分布族，（2）式一般不再成立。非共同支撑分布族是非正则条件的重要情况。卢昆亮首先考虑了一种位置参数双边截断族。非共同支撑的截断族还有其它许多种种重要形式，比如位置刻度参数截断族："等，其中a∈R，γ>0，f(x)是[一1，l]上的正概率密度。所有的截断族都可写成如下一般形式：其中 1

Bahadur表示Bahadur表示就是将样本分位数表示为一种线性和，它能更方便地讨论样本分位数的大样本性质。

样本分位数的Bahadur表示在证明样本分位数的渐近正态性中起到关键性的作用，其原因是：样本分位数是总体分位数的一种非线性和的估计量，Bahadur表示的目标就是将样本分位数表示为一种线性和，从而可以更方便地讨论样本分位数的大样本性质。

Bahadur在独立同分布序列下证明了样本分位数的Bahadur表示，其收敛速度为O(n^−3/4log^1/2nlog^1/4_2n)，其中log2n=loglogn。随后Kiefer证明了其收敛速度为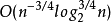 。Sen，Badu和Singh进一步获得了在α-混合序列下样本分位数的Bahadur表示。Yoshihara在φ-混合和α-混合序列下研究了有界样本分位数的Bahadur表示，给出与独立情形几乎相同的收敛速度，并讨论了样本分位数的Bahadur表示的渐进正态性。Sun取消Yoshihara对样本有界的限制，讨论了在α-混合序列下样本分位数的Bahadur表示，并给出多项式衰减形式的收敛速度。同时，Cai和Roussas，Youndje和Vieu也分别研究了在相协和长相依随机过程下分位数光滑估计的大样本性质，Wei和Yang研究了α-混合序列下VaR线性核样本分位数估计的Bahadur表示，并证得收敛速度为log−τn。最近，Ling讨论了在NA序列下样本分位数的Bahadur表示，其收敛速度不超过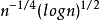，该速度与独立同分布情形相差甚远。2

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学