[科普中国]-球面圆

球面圆(spherical circle)是球面几何的基本概念之一，指球面在空间中与平面相交时的交线圆，包括平面通过球心时交成的球面大圆和平面不通过球心时与球面相交而成的球面小圆1。

基本介绍半球以它的直径为旋转轴，旋转所成的曲面叫做球面。球面所围成的几何体叫做球体，简称球。半圆的圆心叫做球心。连结球心和球面上任意一点的线段叫做球的半径。连结球面上两点并且经过球心的线段叫做球的直径。用一个平面去截一个球，截面是圆面，这个圆面叫做球面圆。经过球心的平面截得的圆叫做大圆。不经过球心的平面截得的圆叫做小圆。

垂直于球面圆所在平面的直径的两个端点(对径点)称为球面圆的球面中心，亦称为球面圆的极。球面大圆的圆弧、优弧、劣弧、余弧、共轭弧依次称为球面大圆弧、大圆优弧、大圆劣弧、余大圆弧、共轭大圆弧。当提到连结球面上非对径的两点的大圆弧时，通常指大圆劣弧，此大圆弧的长度称为此两点间的球面距离，因为球面上非对径的两点与球心不共线而决定一个平面，这两点就在由此平面与球面相交的惟一大圆上，所以上述球面距离的定义适用于球面上非对径的任意两点，至于球面的两个对径点，自然地以半大圆弧的长度作为它们的球面距离，球面圆的球面中心与球面圆上的点的球面距离相等，即球面圆是球面上与一个定点的距离等于定值的点的轨迹，此定点即球面圆的球面中心或极，这个定值称为球面圆的球面半径，亦称为球面圆的角半径、弧半径或极距，球面大圆的球面半径等于一象限弧，球面小圆与两个球面中心(极)相应有小于和大于一象限弧的两个球面半径，球面半径小于一象限弧的极称为近极，另一个称为远极，由于球面小圆的球面中心通常是指离该圆所在平面的距离较近的那个近极，因此，球面小圆的球面半径通常指小于一象限弧的那一个1。

相关概念及性质球的任意直径与球面相交于两点，这两点叫做直径对点2。

定理1通过球面上任意两点(非直径对点)，有且仅有一个大圆。

证明因为过球面上任意两点与球心能决定唯一平面，它与球的交线就是所求的大圆。通过非直径对点A、B的大圆，以大圆B或大圆BA表示，并说它是连结两点A和B的大圆。

定理2同一球面上的两个大圆，必交于两个直径对点。

证明因为两个大圆所在的平面，有一个公共点(球心)，因而它们必交于一直线，这直线与球面的交点，便是两个大圆的交点， 显然它们是直径对点。

从上面两个定理容易看出， 大圆把球面分或两个相等的部分(半球)， 同一球面上的两个大圆交于两点，并且每个大圆都被这两个点分成两个相等的部分(半圆)。

任意大圆上的两点A和B，将大圆分成两部分，都叫做以A、B为端点的大圆弧，若点A和B是直径对点时， 则大圆被它们所分成的两弧相等, 即都是半圆.若点A、B不是直径对点，则以A、B点为端点的两个大圆弧中,有一个所对的圆心角∠AOB( 在大圆所在的平面上)小于平角， 而另--弧所对的圆心角大于平角，这时， 把前一弧叫做大圆的以A、B为端点的劣弧，后一个叫做以A、B为端点的优弧。

如果两个大圆弧所对的圆心角相等，就说两弧相等。

一般说连结两点的大圆弧，一概指劣弧。

以点A、B为端点的大圆弧(劣弧)，叫做球面上两点A和B间的球面距高， 简称A和B的距离。

球面上的一点和以此点为公共端点的两个大圆弧所构成的球面图形，叫做球面角，或简称角，这个点叫做它的顶点，两个大圆弧叫做它的边。

若构成球面角的两个大圆弧，分别通过点B和C,它们的公共顶点是A时，把这个角记作∠BAC或∠CAB(图1)。

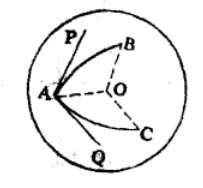
球面角的大小，可以用过顶点两边切线的夹角来度量，显然这两个切线的夹角，就是两大圆弧(边)所在平面构成的二面角的平面角，如图1的二面角B-OA-C的平面角。 因方它们分别垂直于棱OA,因此，球面角∠BAC的大小等于它所对应的面角B-OA-C的大小。

两个球面角，如果它们所对应切线夹角相等时，就说这两个球面角相等.这时它们所对应的二面角也必然相等。类似的可以引入两个球面的“大于” 与“小于”的概念。 也可以引入两角的和、差， 以及直角、 锐角、钝角、 角平分线等概念。

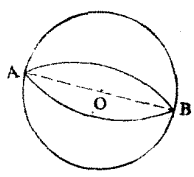
球面上的直径对点， 和以它们为端点的两个半圆所构成的图形，叫做球面二角形。 构成这二角形的半圆叫做它的边，两个直径对点叫做它的顶点， 顶点和边所构成的球面角，叫做二角形的角，显然球面二角形的角相等(图2)。

若两大圆(或大圆弧)的交角是直角时， 则这两个大圆(或大圆弧)叫做垂直(图3)。

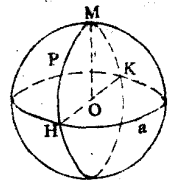
垂直于已知大圆(或小圆)所在平面的直径，在球面上的直径对点，叫做大圆(或小圆)的极。

定理3 通过球面上所设大圆两极以外的一个点， 有一个并且只有一个大圆垂直于已知大圆。

证明 设已知大圆a及不与a的两极重合的点P(图3)，过PO作垂直于大圆a所在平面的平面，这个平面有一个而且只有一个。设这个平面与球交于大圆b，则b垂直于a，并且是唯一的。

定理4 两大圆垂直的必要且充分的条件，是其中一个通过另一个的极。

证明若大圆b过大圆a的极点M, 则因为MO垂直于大圆a所在的平面，显然大圆b所在的平面垂直于大圆a所在的平面，所以a与b的交角是直角，因此充分性成立(图3)，

反之， 若大圆b垂直于大圆a，则两大圆所在的平面垂直。设M为大圆a的极点， 则MO垂直于大圆a所在的平面，而O在大圆b所在的平面上，所以OM在这个平面上，从而b通过点M，因此，必要性也成立。

自已知点到已知大圆所作的垂直大圆弧与已知大圆的两个交点中，其球面距离较近的，叫做已知点到已知大圆的球面距离。

由极的定义可以得出：球面上大圆或小圆上的点，到它的极的球面距离总相等，大圆上的点到它的极的球面距离是大圆周的四分之一”，因此， 大、小圆都可看成是到球面一个定点有等球面距离的点的轨迹2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学