维维亚尼曲线(Viviani curve)是一种特殊曲线,球面x²+y²+z²=a²与圆柱面x²+y²-ax=0的交线。它的参数方程可写作r(t)=(a cos²θ,a cos θ sin θ,a sinθ),θ∈[0,2π],是由球面上经度与纬度相等或成相反数的点组成的。维维亚尼(V.Viviani)在整理和修复佛罗伦萨图书馆所藏的东方学者对阿波罗尼奥斯(Apollonius,(P))所著《圆锥曲线论》第5卷的评注时,于1692年正式提出了佛罗伦萨之迷:求一个教堂的半球形屋顶的面积,在屋顶的四面挖去相同的圆孔形窗户,此即球面与两个柱面的交线,这个问题曾经引起过许多数学家如约翰第一·伯努利(Bernoulli,Johann Ⅰ)、沃利斯(J.Wallis)和洛必达(L′Hospital,G.-F.-A.de)的重视,特别是早在1689年,莱布尼茨(G.W.Leibniz)还从德国到意大利去会见维维亚尼,并用积分法给出此问题的解法1。
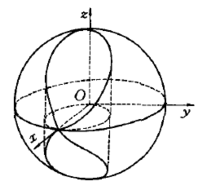
基本介绍维维亚尼曲线是由方程组
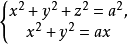 确立的曲线,其中第一个方程代表球面,第二个方程代表圆柱面,维维亚尼曲线即是两个面的交线。
确立的曲线,其中第一个方程代表球面,第二个方程代表圆柱面,维维亚尼曲线即是两个面的交线。
维维亚尼曲线的参数方程由维维亚尼曲线:
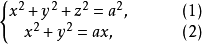
圆柱面的方程即方程(2)可以写为
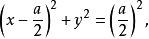 由圆的参数方程可得
由圆的参数方程可得
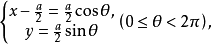 代入
代入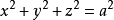 中即得
中即得
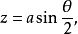 故得所求的交线的参数方程为:
故得所求的交线的参数方程为:
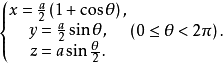
例题解析【例1】一个半径为a的球面与一个直径为小于球面半径的圆柱面,如果圆柱面通过球心,那么这时球面与圆柱面的交线叫做维维安尼(Viviani)曲线,这条曲线的方程可以写为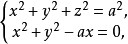 试求此曲线对三个坐标面的射影柱面方程。 .
试求此曲线对三个坐标面的射影柱面方程。 .
分析 求曲线对于坐标面的射影柱的方程一般通过消变量的方法,这里要注意变量的范围2。
解 显见,曲线对xOy面的射影柱面为圆柱面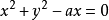 ,
,
消去y得
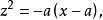 由
由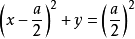 ,知
,知
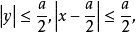 故
故
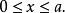
从而曲线对xOz面的射影柱面是抛物柱面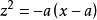 满足
满足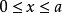 的部分。
的部分。
消去x得
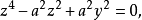 从而曲线对yOz面的射影柱面方程为
从而曲线对yOz面的射影柱面方程为
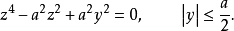
【例2】求维维安尼(Viviani)曲线
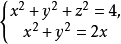 关于三个坐标面的投影柱面。
关于三个坐标面的投影柱面。
解 所给方程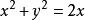 中不含z,故它就是曲线关于XOY面的投影柱面方程,将其化为
中不含z,故它就是曲线关于XOY面的投影柱面方程,将其化为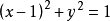 可看出该投影柱面是一个圆柱面,将所给两个方程相减可得
可看出该投影柱面是一个圆柱面,将所给两个方程相减可得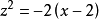 ,可见曲线关于XOZ面的投影柱面是一个抛物柱面,从后一个投影柱面方程解出x,代入前一个投影柱面方程可得
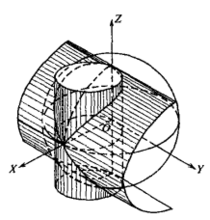
,可见曲线关于XOZ面的投影柱面是一个抛物柱面,从后一个投影柱面方程解出x,代入前一个投影柱面方程可得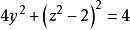 ,这就是曲线关于YOZ面的投影柱面(图2)。
,这就是曲线关于YOZ面的投影柱面(图2)。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国