[科普中国]-卡帕曲线

卡帕曲线是一种由圆产生的曲线，半径为定长a的动圆C的圆心在二轴上滑动。

简介卡帕曲线(Kappa curve)从坐标原点O向圆C所作切线的切点M的轨迹称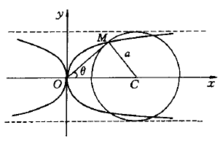为卡帕(K)曲线(见图).它的极坐标方程为p=a cot B，直角坐标方程为y2(x2-f-yz)= a2x2. 17世纪斯吕塞(Sluse，R. -F. de)与惠更斯(Huygens , C.)在通信中第一次提到卡帕曲线.当时是为了解答下面的运动学问题:同一平面内有一个固定的直角坐标系二勿和一个运动的直角坐标系x' Or y'，已知xr轴始终通过点o, y'轴与x轴的交点C到。‘的距离等于定长a，求动坐标系的原点。‘的轨迹.这里的点}r相当于图中的点M，rM,x轴相当于直线MO。

有关研究历史卡帕曲线（kappa curve）也称为Gutschoven曲线1（Gutschoven's curve），是外形类似希腊字母ϰ的二维代数曲线。

Gérard van Gutschoven在1662年就开始研究此一曲线。

Kappa曲线是伊萨克·巴罗第一批用rudimentary calculus来判断曲线切线的曲线之一。

艾萨克·牛顿及约翰·白努利后来也有研究过此曲线。

方程表示Kappa曲线在笛卡儿坐标系下的方程为1

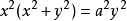
其参数方程为

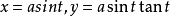
极坐标系的方程简单很多

Kappa曲线有二条垂直的渐近线，为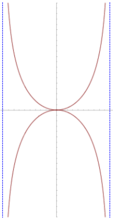

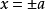
在右图中以虚线表示。

Kappa曲线的曲率：

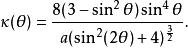
切线角为：

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学