[科普中国]-李亚普诺夫定理

李亚普诺夫定理是关于实矩阵特征值的一个命题，对n阶实矩阵A和n阶正定矩阵C，若存在正定矩阵B，使得AB+BA′=-C，则A的特征值的实部必全小于零，这个定理由李亚普诺夫(А.М.Ляпунов)提出，在运动稳定性理论中起着重要的作用1。

基本介绍李亚普诺夫定理是数学生态学的重要定理之一，是判定系统稳定性质的重要定理，对于复杂生态系统

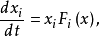设有正平衡点x*，x*∈Ω⊂Rn+，若在区域Ω内定义的函数V(x)对于系统具有性质：

1.V(x*)=0，并且x*是V(x)在Ω内惟一整体最小值；

2.在Ω内，对每一个正值K，曲面族V(x)=K都是闭曲面；

3.导数

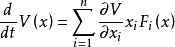对于所有x∈Ω是非正的；则称函数V(x)是系统在Ω内的李亚普诺夫函数。

李亚普诺夫定理断言：若系统有正平衡点x*∈Ω，如果存在李亚普诺夫函数V(x)，在Ω内dV/dt是负定的，则x在区域Ω内为渐近稳定的(即以Ω内任意点为初值的解，当t→∞时趋于x*)，特别当Ω≡Rn+时，x*称为全局渐近稳定的2。

相关说明定理1（李亚普诺夫定理） A的所有特征值都具有负实部,或等价地说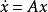， 的零状态是渐近稳定的，当且仅当对于任意给定的正定埃尔米特矩阵N，矩阵方程

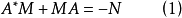具有唯一的埃尔米特解M，并且M是正定的3。

系1 A的所有特征值都具有负实部，或等价地说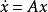， 的零状态是渐近稳定的，当且仅当对于任意给定的，具有{A，N}可观测之性质的，半正定埃尔米特矩阵N，矩阵方程

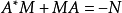有唯一的埃尔米特解M，并且M是正定的。

定理1和系1的含义是，若A是渐近稳定的，且N正定或半正定，则(1)式的解M必为正定，但这并不是说，若A是渐近稳定且M是正定，由(1)式算得的矩阵N是正定或半正定的。

因定理1对于任何正定埃尔米特矩阵N均成立,故(1)式中的矩阵N常选为单位矩阵，由于M是埃尔米特矩阵，故其中有n2个未知数需要求解，若M是实对称矩阵，则其中有n(n+1)/2 个未知数需要求解。因此，矩阵方程(1)实际上包含有n2个线性代数方程，为了应用定理1，我们必须对M求解n2个方程，随后核查M是否正定，这些工作实非易事，因此，定理1及其系一般并不用来确定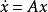 的稳定性。然而，应用李亚普诺夫第二法研究非线性时变系统的稳定性时，定理1却是至关重要的3。

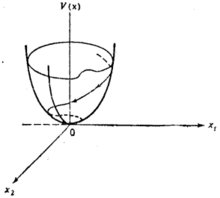
现对李亚普诺夫定理作物理的解释，若埃尔米特矩阵M是正定的，则

V(x)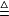 x*Mx， (2)

的曲面呈碗形，如图1所示.现在设想，沿着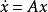 的轨迹连续求取V的值，我们想知道，随着状态沿轨迹移动时， V的值是增加还是减小，沿着 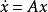的任何轨迹取V关于t的导数，得

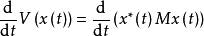
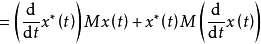
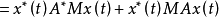
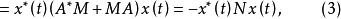其中N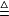 -(A*M+MA)。上式给出了 V(x)沿着 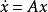的任一轨迹的变化率。若N是正定的，则-x*(t)Nx(t)恒为负，这就意味着，沿 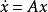的任何轨迹，V(x(t))将随时间而单调下降，所以，当t→∞时，V(x(t))最终将趋于零，因V(x)为正定，故仅在x=0时有V(x)=0，由此断定，若能找到以(1)式相互联系的正定矩阵M和N，则当t→∞时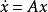， 的每一个轨迹将趋于零向量。函数V(x)称为 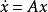的李亚普诺夫函数，李亚普诺夫函数可以认为是距离或能量概念的推广。如果状态的“距离”沿着 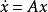的任何轨迹随时间而减小，则当t→∞时，x(t)必将趋于零3。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学