[科普中国]-卡塔朗定理

卡塔朗定理是一个著名的极值问题。自△ABC内的一点作各边的垂线，若以各垂线长作成的正方形面积之和为最小，则该点为连结三垂线垂足所成三角形的重心。

简介卡塔朗定理是一个著名的极值问题。

自△ABC内的一点作各边的垂线，若以各垂线长作成的正方形面积之和为最小，则该点为连结三垂线垂足所成三角形的重心。

举例如图，KD⟘BC，KE⟘AC，KF⟘AB，且KD2+KE2+KF2为最小，则K是垂足△H1H2H3的重心。此点又是原三角形的类似重心。1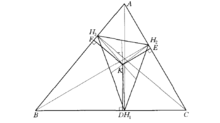

卡塔朗卡塔朗一生共发表200多种涉及各数学领域的论著，在微分几何中，他证明了下列所谓卡塔朗定理：当一个直纹曲线是平面和一般的螺旋面时，它只能是实的极小曲面，他还和雅可比(Jacobi,C.G.J.)同时解决了多重积分的变量替换问题，建立了有关的公式。此外，他还在函数论、伯努利数和其他领域也做出了一定的贡献。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学