[科普中国]-三角形不等式

三角形不等式(triangular inequality)可以指三角形边长关系的不等式，也可以指三角形边长关系的推广，即以三角形边长关系的不等式这一几何事实为背景的不等式。

基本介绍下面是三角形不等式的几种解释：
（1）如果A与B是不同的两个点，线段AB的长称为这两点之间的距离，假如点A与点B相重合，则这两点之间的距离为零。下面定理所叙述的关于三点之间距离的性质称为三角形不等式1。

定理 若A、B、C为任意三点，不一定是三个不同的点，则距离AB不应大于两距离之和AC+CB。

（2）以三角形的任两边之和总大于第三边这一几何事实为背景的不等式叫做三角形不等式，例如，距离公理中的2

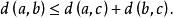
（3）三角形不等式指形如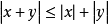的不等式，其中x、y为实数或复数。当x、y是复数时，它等价于三角形的一条边长小于另外两条边长之和，故得此名。在赋范线性空间中．三角形不等式形如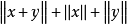，其中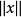表示该空间的元素(向量)x的范数。特别在n维欧几里得空间中。其形式为3

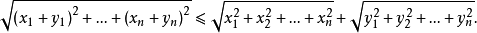
（4）三角形不等式也可以指三角形边长关系的推广，设V是欧氏空间，对V中任意两个向量α，β，|α+β|≤|α|+|β|，此不等式称为三角形不等式4。一般地，设α1，α2，…，αm是欧氏空间的m个向量，则：

|α1+α2+…+αm|≤|α1|+|α2|+…+|αm|.

三角形不等式亦可表示为：

|α-β|≤|α-γ|+|γ-β|.

推广此不等式，则得到托勒密不等式

|α-β|·|γ|≤|β-γ|·|α|+|γ-α|·|β|.4

例题解析下面问题里,a,b和c表示任意三角形的边长5。

【例1】证明:a=y+z,b=x+z,c=x+y,其中x,y和z是正数。

提示解方程组x+y=c,x+z=b,y+z= a,得出

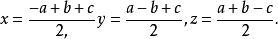由三角形不等式得出x,y,z都是正数。

【例2】证明:a²+ b²+c²

提示 根据三角形不等式有：

a²>(b-c)²=b²-2bc+c²，

b²>a²-2ac+c²，

c²>a²-2ab + b²，

将这三个不等式相加，即得所证。

【例3】对任意自然数n，数an, bn和cn可以构成三角形，证明:数a,b和c中有两个相等。

提示 可以认为a≥b≥c，我们证明a = b，实际上，如果b

提示 因为c(a-b)²+4abc=c(a+b)²,所以

a(b-c)²+b(c-a)²+c(a-b)²+4abc- a³-b³-c³=a((b-c)²-a²)+b((c- a)²-b²)+c((a-b)²-c²) =(a+b-c)(a-b+c)(-a+b+c)

(最后的等式用简单的计算来检验)，根据三角形不等式，全部三个因子都是正数5。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学